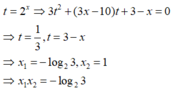4x-10.2x+16=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 8 2019
Đáp án D
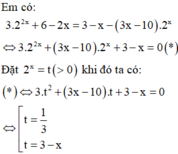
Coi là phương trình bậc hai ẩn t, tính ∆ theo biến em có:
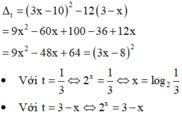
Xét hàm số f x = 2 x đồng biến trên − ∞ ; + ∞ , hàm số g x = 3 − x nghịch biến trên − ∞ ; + ∞
Mà f(1) = g(1) => Phương trình có nghiệm duy nhất x = 1
Vậy phương trình (*) có 2 nghiệm => tổng các nghiệm là
1 + log 2 1 3 = log 2 2 + log 2 1 3 = log 2 2 3
X
18 tháng 2 2020
Mấy câu này khá giống nhau nhé anh (câu 1 giống câu 4 và 5, cấu 2 giống câu 3) =)))
Câu 1: 2x - 7 + (x - 14) = 0
<=> 3x -21 = 0
<=> 3x = 21 => x = 7
Câu 2:
x2 - 6x = 0 <=> x.(x - 6) = 0 => \(\orbr{\begin{cases}x=0\\x-6=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=6\end{cases}}\)
Chúc anh học tốt !!!
18 tháng 2 2020
Câu 1, 2 có người làm rồi nên mik làm tiếp cho mấy câu tiếp. Cứ áp dụng A.B = 0 => A = 0 hoặc B = 0
3; ( x - 3 )( 16 - 4x ) = 0
=> x - 3 = 0 hoặc 16 - 4x = 0
=> x = 3 hoặc x = 4
Vậy x = 3 hoặc x = 4.
4; ( x - 3 ) - ( 16 - 4x ) = 0
=> x - 3 - 16 + 4x = 0
=> ( x + 4x ) - ( 3 + 16 ) = 0
=> 5x - 19 = 0
=> x = 19/5
Vậy x = 19/5
5; ( x + 3 ) + ( 16 - 4x ) = 0
=> x + 3 + 16 - 4x = 0
=> ( x - 4x ) + ( 16 + 3 ) = 0
=> 3x + 19 = 0
=> x = 19/3
Vậy x = 19/3
3 tháng 7 2016
\(4x^2-16=0\)
\(=>\left(2x\right)^2-4^2=0\)
\(=>\left(2x-4\right)\left(2x+4\right)=0\)
\(=>\orbr{\begin{cases}2x-4=0\\2x+4=0\end{cases}=>\orbr{\begin{cases}x=\frac{4}{2}=2\\x=\frac{-4}{2}=-2\end{cases}}}\)
Ủng hộ nha
Thanks
VP
3
KK
6 tháng 9 2021
1. \(\sqrt{x^2-4x+3}=x-2\)
<=> x2 - 4x + 3 = (x - 2)2
<=> x2 - 4x + 3 = x2 - 4x + 4
<=> x2 - x2 - 4x + 4x = 1
<=> 0 = 1 (Vô lí)
vậy PT có nghiệm là S = \(\varnothing\)
KK
6 tháng 9 2021
2. \(\sqrt{4x^2-4x+1}=x-1\)
<=> \(\sqrt{\left(2x-1\right)^2}=x-1\)
<=> 2x - 1 = x - 1
<=> 2x - x = -1 + 1
<=> x = 0
NV
21 tháng 6 2016
(x - 3)(2x - 6)(4x - 16) = 0
=> x - 3 = 0 => x = 3
hoặc 2x - 6 = 0 => x - 3 = 0 => x = 3
hoặc 4x - 16 = 0 => x - 4 = 0 => x = 4
Vậy x = 3 . x = 4
NQ
4
C
5 tháng 5 2023
`(2x-6)(4x+16)=0`
`@TH1:`
`2x-6=0`
`<=>2x=6`
`<=>x=3`
`@TH2:`
`4x+16=0`
`<=>4x=-16`
`<=>x=-4`
R
5 tháng 5 2023
\(\left(2x-6\right).\left(4x+16\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-6=0\\4x+16=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=6\\4x=-16\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
\(S=\left\{3;-4\right\}\)
31 tháng 7 2018
\(x^3+4x-16=x^3-2x^2+2x^2-4x+8x-16\)
\(=x^2\left(x-2\right)+2x\left(x-2\right)+8\left(x-2\right)\)
\(=\left(x^2+2x+8\right)\left(x-2\right)\)
Mà \(x^3+4x-16=0\Rightarrow\left(x^2+2x+8\right)\left(x-2\right)=0\) (1)
Mặt khác, \(x^2+2x+8=x^2+2x+1+7=\left(x+1\right)^2+7>0\) \(\forall x\) (2)
Từ (1) và (2)\(\Rightarrow x-2=0\Rightarrow x=2\)
Vậy \(x=2\)
Chúc bạn học tốt.