64x2+y4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1
30 tháng 6 2021
$a)64x^2-49=(8x)^2-7^2=(8x-7)(8x+7)\\b)-a^2b^2+36=6^2-(ab)^2=(6-ab)(6+ab)\\c)225-(x-11)^2=(15-x+11)(15+x-11)=(x+4)(26-x)\\d)x^2-8x+12=x^2-2x-6x+12=x(x-2)-6(x-2)=(x-2)(x-6)$
Y
19 tháng 6 2023
\(a,64x^2-\left(8a+b\right)^2\)
\(=\left(8x\right)^2-\left(8a+b\right)^2\)
\(=\left[8x-\left(8a+b\right)\right]\left(8x+8a+b\right)\)
\(=\left(8x-8a-b\right)\left(8x+8a+b\right)\)
\(b,\dfrac{12}{5}x^2y^2-9x^2-\dfrac{4}{25}y^2\)
\(=-\left(9x^2-\dfrac{12}{5}x^2y^2+\dfrac{4}{25}y^2\right)\)
\(=-\left[\left(3x\right)^2-2.3.\dfrac{2}{5}x^2y^2+\left(\dfrac{2}{5}y\right)^2\right]\)
\(=-\left(3x-\dfrac{2}{5}y\right)^2\)
CM
18 tháng 6 2017
Ta có: 2 x + y 2 − 5 4 x 2 − y 2 + 6 4 x 2 − 4 x y + y 2 = 0 ( 1 ) 2 x + y + 1 2 x − y = 3
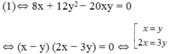
Với x = y ta có 2 ⇒ 3 x + 1 x = 3 ⇔ 3 x 2 - 3 x + 1 = 0 : phương trình vô nghiệm.
Với 2 x = 3 y ta có 2 ⇒ 4 y + 1 2 y = 3 ⇔ 8 y 2 - 6 y + 1 = 0 ⇔ y = 1 2 y = 1 4
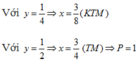
Đáp án cần chọn là: A
23 tháng 7 2023
A) \(...=\left(7y-3\right)^3\)
B) \(...=\left(4y-3\right)^3\)
C) \(...=x^4+2x^2+1-\left(y^2+2y+1\right)\)
\(=\left(x^2+1\right)^2-\left(y+1\right)^2\)
D) \(...=x^2-6x+9-\left(y^2-10y+25\right)\)
\(=\left(x-3\right)^2-\left(y-5\right)^2\)
CM
29 tháng 3 2018
x3y4 - 5y8 + x3y4 + xy4 + x3 - y2 - xy4 + 5y8
= (x3y4 + x3y4) + (xy4 – xy4) + (-5y8 + 5y8) + x3 – y2
= (1+ 1)x3y4 + (1 – 1).xy4 + ( - 5+ 5)y8 + x3 – y2
= 2x3y4 + x3 - y2.
Đa thức có bậc là 7.
OT
1
DD
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
\(P=\left(x^4+y^4+\dfrac{1}{256}+\dfrac{255}{256}\right)\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)\)
\(P=\left(x^4+y^4+\dfrac{1}{256}\right)\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)+\dfrac{255}{256}\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)\)
\(P\ge\left(\dfrac{x^2}{x^2}+\dfrac{y^2}{y^2}+\dfrac{1}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{2}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)^2+1\right)\)
\(P\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{2}\left(\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right)^2+1\right)\)
\(P\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{8}\left(\dfrac{4}{x+y}\right)^4+1\right)\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{4^4}{8}+1\right)=\dfrac{297}{8}\)
\(P_{min}=\dfrac{297}{8}\) khi \(x=y=\dfrac{1}{2}\)
64x^4+y^4
=(8x^2)^2+(y^2)^2
=[(8x^2)^2+16x^2y^2+(y^2)^2]-16x^2y^2
=(8x^2+y^2)-(4xy)^2
=(8x^2+y^2-4xy)(8x^2+y^2+4xy)