Chứng minh rằng số đo góc của n-giác đều là
\(\frac{\left(n-2\right).180^o}{n}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 4 2017
a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)
CM
7 tháng 10 2017
a)Vẽ các đường chéo xuất phát từ một đỉnh của n - giác, ta được (n - 2) tam giác.
Tổng các góc của hình n - giác bằng tổng các góc của (n - 2) tam giác, tức là có số đo bằng (n - 2).1800.
b) ta có: (n - 2).1800 = (12 - 2 ).1800 = 18000
21 tháng 9 2023
Tham khảo:
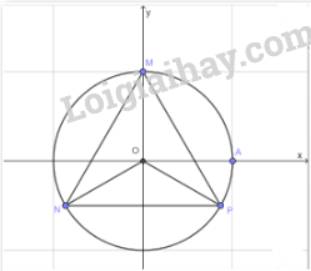
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
26 tháng 9 2023
công thức này sai ngay tầng một rồi còn chứng minh kiểu gì n=1 số tam giác là 9/8
DD
29 tháng 9 2016
\(\text{Bn hỏi từ từ từng câu 1 thôi}\)
\(\text{Bn hỏi thế ai mà dám làm}\)
~~~~~~~~~~~~~
~~~~~~~~~~~
~~~~~~~~~~~~
29 tháng 9 2016
Chí lí
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
sọ ghi 2 hàng khoogn đc tích tăng lê hiều hàng
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~````
PT
1
CM
15 tháng 7 2018
Vẽ một n-giác lồi, kẻ các đường chéo xuất phát từ một đỉnh của n-giác lồi thì chia đa giác đó thành (n - 2) tam giác.
Tổng các góc của n-giác lồi bằng tổng các góc của (n - 2) tam giác bằng (n - 2).180o.
Hình n-gíác đều có n góc bằng nhau nên số đo mỗi góc bằng:
n - 2 . 180 0 n
tai vi cu n giac tao thanh n-2 tam giac
HS tự CM