 tìm đkxđ giúp mik v
tìm đkxđ giúp mik v
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Biểu thức này không có GTLN vì nếu cho x > 1 và \(x\rightarrow1\Rightarrow\dfrac{1}{\sqrt{x}-1}\rightarrow\infty\).


\(\sqrt{\dfrac{1}{x^2-2x+1}}=\sqrt{\dfrac{1}{\left(x-1\right)^2}}\)
ĐKXĐ: \(\left(x-1\right)^2\ne0\Leftrightarrow x\ne1\)
Vậy \(x\in R,x\ne1\) thì căn thức xác định

a: \(P=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b: \(P-1=\dfrac{\sqrt{a}-1-\sqrt{a}}{\sqrt{a}}=\dfrac{-1}{\sqrt{a}}< 0\)

\(19,ĐKXĐ:\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}\ge0;x\ne5\\ \Leftrightarrow5-x< 0\left(-2\sqrt{6}+\sqrt{23}< 0\right)\\ \Leftrightarrow x>5\)
\(21,ĐKXĐ:x\ne7;\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}\ge0\\ \Leftrightarrow x-7>0\left(2\sqrt{15}-\sqrt{59}>0\right)\\ \Leftrightarrow x>7\)
\(23,ĐKXĐ:49x^2-24x+4\ge0\Leftrightarrow\left(49x^2-14\cdot\dfrac{12}{7}x+\dfrac{144}{49}\right)+\dfrac{52}{49}\ge0\\ \Leftrightarrow\left(7x-\dfrac{12}{7}\right)^2+\dfrac{52}{49}\ge0\\ \Leftrightarrow x\in R\)

ĐIều kiện:`x^2-7x+8>=0`
`<=>x^2-2*x*7/2+49/4-17/4>=0`
`<=>(x-7/2)^2-17/4>=0`
`<=>(x-7/2)^2>=17/4`
`<=>|x-7/2|>=sqrt{17}/2`
`<=>` \(\left[ \begin{array}{l}x \ge \dfrac{7+\sqrt{17}}{2}\\x \le \dfrac{-\sqrt{17}+7}{2}\end{array} \right.\)
`pt<=>x^2-7x+sqrt{x^2-7x+8}-12=0`
`<=>x^2-7x+8+sqrt{x^2-7x+8}-20=0`
Đặt `a=sqrt{x^2-7x+8}(a>=0)`
`pt<=>a^2+a-20=0`
`<=>a=4(tm),a=-5(l)`
`<=>x^2-7x+8=16`
`<=>x^2-7x-8=0`
`a-b+c=0`
`=>x_1=-1(tm),x_2=8(tm)`
Vậy `S={-1,8}`

\(P=\dfrac{\sqrt{x}-2}{\sqrt{x}}=1-\dfrac{2}{\sqrt{x}}\)
Vì \(x\le3\Rightarrow\dfrac{2}{\sqrt{x}}\ge\dfrac{2}{\sqrt{3}}\)\(\Leftrightarrow-\dfrac{2}{\sqrt{x}}\le-\dfrac{2}{\sqrt{3}}\)\(\Leftrightarrow1-\dfrac{2}{\sqrt{3}}\le1-\dfrac{2}{\sqrt{3}}\)
\(\Rightarrow\)\(P\le\dfrac{3-2\sqrt{3}}{3}\)
Dấu = xra khi x=3
Vậy \(P_{max}=\dfrac{3-2\sqrt{3}}{3}\)

điều kiện xđ:
x khác ( -2,2,0)
A=\(\left(\frac{1}{x+2}+\frac{1}{x-2}\right):x-\frac{2}{x}\)
=\(\left(\frac{x-2+x+2}{x^2-4}\right):x-\frac{2}{x}\)
=\(\frac{2}{x^2-4}-\frac{2}{x}=\frac{2x-2x^2+8}{x\left(x^2-4\right)}\)

\(A=\left(\frac{1}{x+2}+\frac{1}{x-2}\right)\times\frac{x-2}{x}\)
a) ĐKXĐ : \(x\ne0;x\ne-2;x\ne2\)
b) Rút gọn:
\(A=\frac{x-2+x+2}{\left(x+2\right)\left(x-2\right)}\times\frac{x-2}{x}=\frac{2}{x+2}\)
c) Tìm x>0 để: \(A>\frac{1}{2}\Rightarrow\frac{2}{x+2}>\frac{1}{2}\)Do x>0 nên x + 2 >0 => x + 2 <4 =>x < 2.
Vậy, với x dương để A > 1/2 thì x<2
d) A nguyên thì 2 chia hết cho x+2 hay x+2 thuộc U(2) = {-2;-1;1;2)
- x + 2 = -2 => x = -4
- x + 2 = -1 => x = -3
- x + 2 = 1 => x = -1
- x + 2 = 2 => x = 0
Có 4 giá trị nguyên của x là: -4; -3; -1; 0 để A có giá trị nguyên.
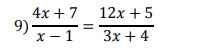

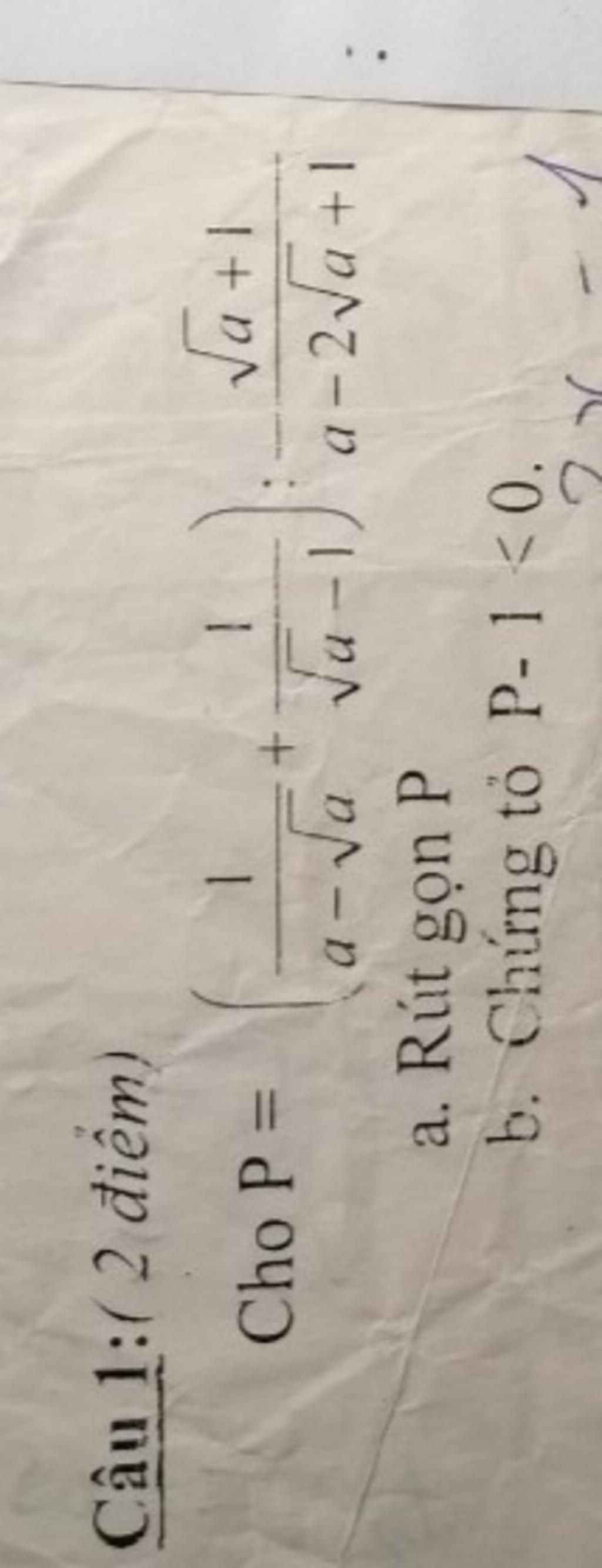
 giải giúp mình câu 19,21,23,24,18,10,13 với
giải giúp mình câu 19,21,23,24,18,10,13 với

a, đk \(\left\{{}\begin{matrix}x^2-4x+4\ge0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\left(dung\right)\\x\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in R\\x\ne3\end{matrix}\right.\)
b, đk \(\left\{{}\begin{matrix}2x-3>0\\x-7>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{3}{2}\\x>7\end{matrix}\right.\Leftrightarrow x>7\)
c, đk \(x-10\sqrt{x}+25>0\Leftrightarrow\left(\sqrt{x}-5\right)^2>0\Rightarrow x\ne25\)