cho hai số thực x>0,y>0 thoả mãn xy=6.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
0
CM
28 tháng 12 2019
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được :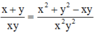 
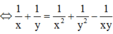
Đặt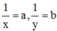 
ta có 
Khi đó 
Ta có 
mà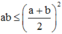 
nên 
Dấu đẳng thức xảy ra khi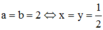 
. Vậy Mmax = 16
AH
Akai Haruma
Giáo viên
30 tháng 6 2023
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
ND
1
29 tháng 3 2019
Áp dụng bđt Cô-si \(1=x^2+y^2\ge2xy\)
\(\Rightarrow xy\le\frac{1}{2}\)
Ta có \(A=\frac{-2xy}{1+xy}\ge\frac{-\frac{2.1}{2}}{1+\frac{1}{2}}=-\frac{2}{3}\)
\("="\Leftrightarrow x=y=\frac{1}{\sqrt{2}}\)
NH
30 tháng 4 2018
\(Q=\frac{3x+3y+2z}{\sqrt{6\left(x^2+5\right)}+\sqrt{6\left(y^2+5\right)}+\sqrt{z^2+5}}\)
\(\Leftrightarrow Q=\frac{3x+3y+2z}{\sqrt{6\left(x^2+xy+yz+zx\right)}+\sqrt{6\left(y^2+xy+yz+zx\right)}+\sqrt{z^2+xy+yz+zx}}\)
\(\Leftrightarrow Q=\frac{3x+3y+2z}{\sqrt{3\left(x+y\right).2\left(x+z\right)}+\sqrt{3\left(y+x\right).2\left(y+z\right)}+\sqrt{\left(z+x\right).\left(z+y\right)}}\)
\(\Rightarrow Q\ge\frac{3x+3y+2z}{\frac{3\left(x+y\right)+2\left(x+z\right)}{2}+\frac{3\left(y+x\right)+2\left(y+z\right)}{2}+\frac{\left(z+x\right)+\left(z+y\right)}{2}}\)
\(\Rightarrow Q\ge\frac{3x+3y+2z}{\frac{9x+9y+6z}{2}}=\frac{2}{3}\)
Dấu "=" xảy ra khi \(x=y=1\)và \(z=2\)
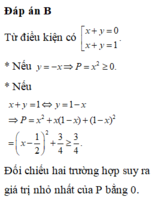
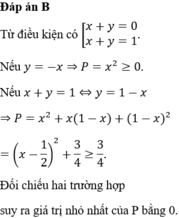
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )