Cho hình dưới, chứng minh ABMN là hình bình hành:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2017
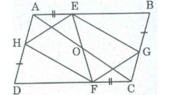
+) Ta có: AH + HD = AD
CG + GB = CB
Mà AD = CB ( vì ABCD là hình bình hành).
DH = GB ( giả thiết)
Suy ra: AH = CG.
Xét ∆ AEH và ∆ CFG:
AE = CF (gt)
∠ A = ∠ C (tính chất hình bình hành)
AH = CG ( chứng minh trên).
Do đó: ∆ AEH = ∆ CFG (c.g.c)
⇒ EH = FG
Xét ∆ BEG và ∆ DFH, ta có:
BG = DH (gt)
∠ B = ∠ D (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF nên AB – AE = CD – CF hay BE = DF )
Do đó: ∆ BEG = ∆ DFH (c.g.c) ⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau)
25 tháng 8 2021
a: Xét ΔHDC có
N là trung điểm của HD
M là trung điểm của HC
Do đó: NM là đường trung bình của ΔHDC
Suy ra: NM//DC và \(NM=\dfrac{CD}{2}\)
mà AB//DC và \(AB=\dfrac{CD}{2}\)
nên NM//AB và NM=AB
b: Xét tứ giác ABMN có
AB//NM
AB=NM
Do đó: ABMN là hình bình hành
H
26 tháng 9 2021
a, Ta có tam giác ABC cân tại A có
AM là đg trung tuyến đồng thời là đg cao
Xét tứ giác ANCM có
D là trung điểm của AC ( gt)
D là trung điểm của MN ( N đối xứng M qua D-gt)
=> ANCM là hình bình hành
mà có góc AMC = 90 độ ( AM là đg cao-cmt)
=> ANCM là hình chữ nhật
H
26 tháng 9 2021
b, Ta có AMCN là hình chữ nhật (cmt)
=> MN = AC ; NA = MC
Ta có
AB = AC ( tam giác ABC là tam giác cân -gt)
mà MN = AC (cmt)
=> AB = MN
Lại có MC = MB ( AM là trung tuyến -gt)
mà MC = AN ( cmt)
=> MB = AN
Xét tứ giác ANBM có
MN = AB (cmt)
NA = MB ( cmt)
=> NABM là hình bình hành (dhnb)
21 tháng 12 2023
a: Ta có: BC=DA(BADC là hình bình hành)
\(MB=MC=\dfrac{BC}{2}\)(M là trung điểm của BC)
\(NA=ND=\dfrac{AD}{2}\)(N là trung điểm của AD)
Do đó: MB=MC=NA=ND
Xét tứ giác ABMN có
BM//AN
BM=AN
Do đó: ABMN là hình bình hành
b: Hình bình hành ABMN có BA=BM(=BC/2)
nên ABMN là hình thoi
c: Ta có: MB//AD
=>\(\widehat{EBM}=\widehat{EAD}\)(hai góc đồng vị)
mà \(\widehat{EAD}=60^0\)
nên \(\widehat{EBM}=60^0\)
Ta có: BA=BE
BA=BM(=BC/2)
Do đó: BE=BM
Xét ΔBEM có BE=BM và \(\widehat{EBM}=60^0\)
nên ΔBEM đều
=>\(\widehat{BEM}=60^0\)
Xét tứ giác ANME có NM//AE(ABMN là hình thoi)
nên ANME là hình thang
Hình thang ANME(NM//AE) có \(\widehat{MEA}=\widehat{A}\left(=60^0\right)\)
nên ANME là hình thang cân
=>AM=NE
21 tháng 12 2021
\(a,\) Vì AM là trung tuyến tam giác cân tại A nên AM cũng là đường cao
Vì D là trung điểm AC và MN nên AMCN là hình bình hành
Mà \(AM\bot BC\Rightarrow AM\bot MC\)
Do đó: AMCN là hình chữ nhật
\(b,\) Vì AMCN là hcn nên \(AM=AC;AN=MC\)
Mà \(AB=AC;MB=MC\Rightarrow AM=AB;AN=MB\)
Vậy ABMN là hình bình hành
\(c,\) Ta có \(BM=MC=\dfrac{1}{2}BC=3(cm)\)
Áp dụng PTG vào tam giác ABM vuông M
\(AM=\sqrt{AB^2-BM^2}=4\left(cm\right)\)
Do đó \(S_{AMCN}=AM\cdot MC=4\cdot3=12\left(cm^2\right)\)
21 tháng 12 2021
a) Xét tam giác ABC cân tại A: AM là trung tuyến (gt).
\(\Rightarrow\) AM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) AM \(\perp\) BC. \(\Rightarrow\) \(\widehat{AMC}\) = 90o.
Xét tứ giác AMCN có:
+ D là trung điểm của MN (N đối xứng với M qua D).
+ D là trung điểm của AC (gt).
\(\Rightarrow\) Tứ giác AMCN là hình bình hành (dhnb).
Lại có: \(\widehat{AMC}\) = 90o (cmt).
\(\Rightarrow\) Tứ giác AMCN là hình chữ nhật (dhnb).
b) Tứ giác AMCN là hình chữ nhật (cmt).
\(\Rightarrow\) AN // MC (Tính chất hình chữ nhật).
\(\Rightarrow\) AN // BM.
Vì AM là trung tuyến của tam giác ABC (gt). \(\Rightarrow\) M là trung điểm của BC.
\(\Rightarrow\) BM = MC = \(\dfrac{1}{2}\)BC.
Mà AN = MC (Tứ giác AMCN là hình chữ nhật).
\(\Rightarrow\) BM = MC = AN.
Xét tứ giác ABMN có:
+ BM = AN (cmt).
+ BM // AN (cmt).
\(\Rightarrow\) Tứ giác ABMN là hình bình hành (dhnb).
c) Ta có: BM = MC = \(\dfrac{1}{2}\)BC = \(\dfrac{1}{2}\).6 = 3 (cm).
Xét tam giác AMB vuông tại M có:
AB2 = AM2 + BM2 (Định lý Pytago).
Thay số: 52 = AM2 + 32.
\(\Leftrightarrow\) 25 = AM2 + 9. \(\Leftrightarrow\) AM2 = 16. \(\Leftrightarrow\) AM = 4 (cm).
Diện tích hình chữ nhật AMCN là: 3 . 4 = 12 (cm2).
14 tháng 7 2021
a) Xét tứ giác AEMF có
\(\widehat{EAF}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{AFM}=90^0\)(gt)
Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
14 tháng 7 2021
b) Xét ΔABC có
M là trung điểm của BC(gt)
MF//AB(cùng vuông góc với AC)
Do đó: F là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
F là trung điểm của AC(cmt)
Do đó: MF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: \(MF=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà AE=MF(AFME là hình chữ nhật)
nên \(AE=\dfrac{AB}{2}\)
mà A,E,B thẳng hàng(gt)
nên E là trung điểm của AB
Ta có: F là trung điểm của NM(gt)
nên \(MN=2\cdot MF\)(1)
Ta có: E là trung điểm của AB(cmt)
nên AB=2AE(2)
Ta có: AEMF là hình chữ nhật(cmt)
nên MF=AE(Hai cạnh đối)(3)
Từ (1), (2) và (3) suy ra MN=AB
Xét tứ giác ABMN có
MN//AB(cùng vuông góc với AC)
MN=AB(cmt)
Do đó: ABMN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
PT
1
CM
16 tháng 12 2018
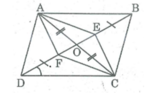
Gọi O là giao điểm của AC và BD, ta có:
OB = OE + EB và OD = OF+ FD (1)
Lại có: EB = FD (giả thiết) (2)
OB = OD ( tính chất hình bình hành). (3)
Từ (1), (2),(3) suy ra: OE = OF
Suy ra tứ giác AECF là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AE // CF.