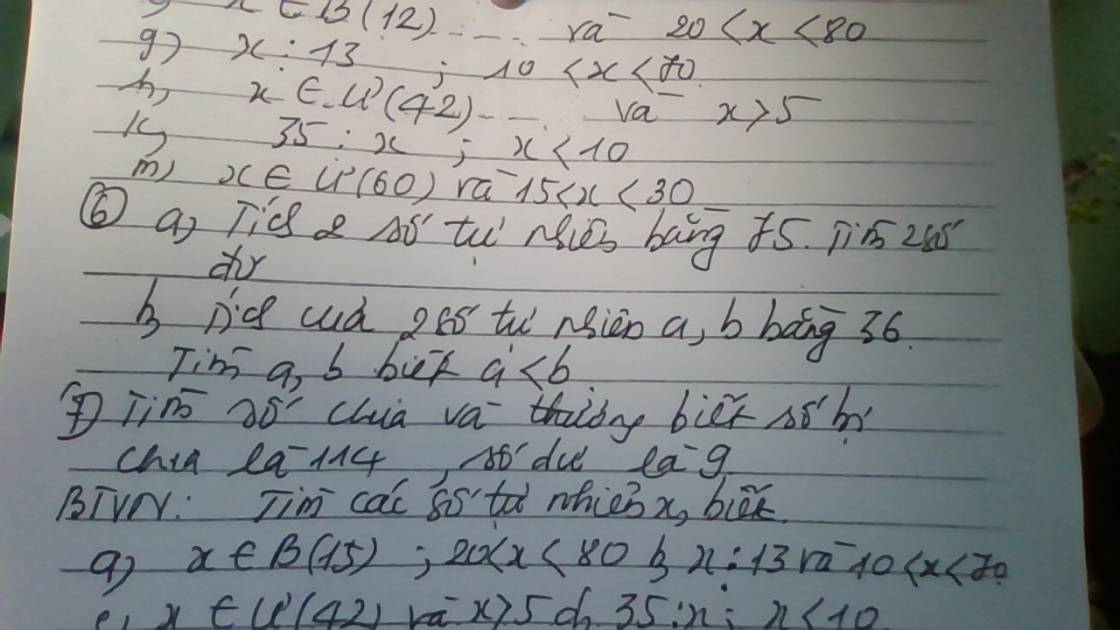Làm hộ mình từ bài 5 trở Đi với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
13 tháng 10 2023
Bài 5
h) x ∈ Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
Mà x > 5
⇒ x ∈ {6; 7; 14; 21; 42}
k) 35 ⋮ x
⇒ x ∈ Ư(35) = {1; 5; 7; 35}
Mà x < 10
⇒ x ∈ {1; 5; 7}
m) x ∈ Ư(60) = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60}
Mà 15 < x < 30
⇒ x = 20
13 tháng 10 2023
h) x ∈ Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
Mà x > 5
⇒ x ∈ {6; 7; 14; 21; 42}
k) 35 ⋮ x
⇒ x ∈ Ư(35) = {1; 5; 7; 35}
Mà x < 10
⇒ x ∈ {1; 5; 7}
m) x ∈ Ư(60) = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60}
Mà 15 < x < 30
⇒ x = 20
31 tháng 10 2021
\(2,\\ a,=2x^2+4x-3x-6-2x^2-4x-2=-3x-8\\ b,=\left[x-2+2\left(x+1\right)\right]^2=\left(x-2+2x+2\right)^2=9x^2\)
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
30 tháng 3 2021
Câu IV:
1) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,F,E,C cùng nằm trên 1 đường tròn(đpcm)
