bài 1 tính (27)^10+(9)^5/9^13+27^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LD
2
H9
HT.Phong (9A5)
CTVHS
15 tháng 10 2023
\(\dfrac{27^{10}+9^5}{9^{13}+27^2}\)
\(=\dfrac{\left(3^3\right)^{10}+\left(3^2\right)^5}{\left(3^2\right)^{13}+\left(3^3\right)^2}\)
\(=\dfrac{3^{30}+3^{10}}{3^{26}+3^6}\)
\(=\dfrac{3^{10}\cdot\left(3^{20}+1\right)}{3^6\cdot\left(3^{20}+1\right)}\)
\(=\dfrac{3^{10}}{3^6}\)
\(=3^{10-6}\)
\(=3^4\)
ND
2
H
27 tháng 9 2023
\(A=\dfrac{27^{10}+9^5}{9^{13}+27^2}\\ =\dfrac{\left(3^3\right)^{10}+\left(3^2\right)^5}{\left(3^2\right)^{13}+\left(3^3\right)^2}\\ =\dfrac{3^{30}+3^{10}}{3^{26}+3^6}\\ =\dfrac{3^{10}\left(3^{20}+1\right)}{3^6\left(3^{20}+1\right)}\\ =\dfrac{3^{10}}{3^6}\\=3^4\\ =81\)
27 tháng 9 2023
\(A=\dfrac{27^{10}+9^5}{9^{13}+27^2}\)
\(A=\dfrac{\left(3^3\right)^{10}+\left(3^2\right)^5}{\left(3^2\right)^{13}+\left(3^3\right)^2}\)
\(A=\dfrac{3^{30}+3^{10}}{3^{26}+3^6}\)
\(A=\dfrac{3^{10}+\left(3^{20}+1\right)}{3^6.\left(3^{20}+1\right)}\)
\(A=\dfrac{3^{10}}{3^6}\)
\(A=3^4\)
\(A=81\)
10 tháng 7 2023
1: =-2/9(15/17+2/17)=-2/9
2: \(=\dfrac{-6}{3}+\dfrac{-21}{90}\)
=-2-7/30=-67/30
3: \(=\dfrac{3}{4}\cdot\dfrac{7}{5}+\dfrac{9}{7}\cdot\dfrac{3}{2}\)
=21/20+27/14=417/140
4: =-25/13(5/19+14/19)=-25/13
5: =-7/5-45/21=-7/5-15/7=-124/35
10 tháng 7 2023
1: =-2/9(15/17+2/17)=-2/9
2: =−63+−2190=−63+−2190
=-2-7/30=-67/30
3: =34⋅75+97⋅32=34⋅75+97⋅32
=21/20+27/14=417/140
4: =-25/13(5/19+14/19)=-25/13
5: =-7/5-45/21=-7/5-15/7=-124/35
25 tháng 4 2018
a, 1/2 x ( 2/9 + 3/7 - 5/27 )
= 1/2 x ( 41/63 - 5/27 )
= 1/2 x 88/189
= 44/189
b, (-5/8 + 1,75 + 8/35) : (-3 và 9/10)
= (-5/8 + 7/4 + 8/35) : (-39/10)
= (9/8 + 8/35) : (-39/10)
=379/280 : (-39/10)
= -379/1092
c, 1/3 x 5/7 - 5/27 x 36/14
= 5/21 - 10/21
= -5/21
Chúc bạn học tốt !
25 tháng 4 2018
a) 1/2 x (\(\frac{42}{189}-\frac{81}{189}-\frac{35}{189}\))=1/2 x 88/189 = 44/189
b) ( \(\frac{-5}{8}+\frac{7}{4}+\frac{8}{35}\)) : \(-3\frac{9}{10}\)
= ( \(\frac{-175}{280}+\frac{490}{280}+\frac{64}{280}\)) : \(\frac{-39}{10}\)
=\(\frac{379}{280}\) x \(\frac{-10}{39}\)=\(\frac{-379}{1092}\)
c) \(\frac{5}{21}\)- \(\frac{10}{21}\)= \(\frac{-5}{21}\)
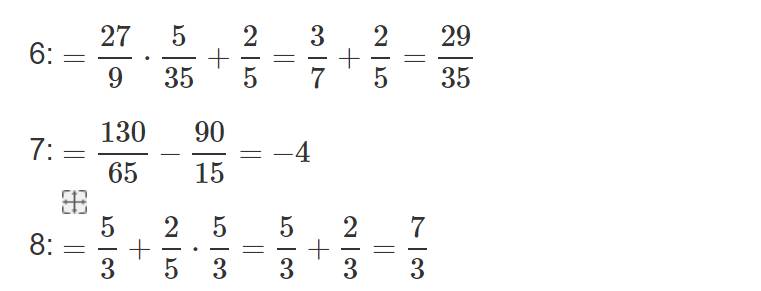
`[27^10+9^5]/[9^13+27^2]`
`=[(3^3)^10+(3^2)^5]/[(3^2)^13+(3^3)^2]`
`=[3^30+3^10]/[3^26+3^6]`
`=[3^6(3^24+3^4)]/[3^6(3^20+1)]`
`=[3^24+3^4]/[3^20+1]`
`=81`