Tìm x biết (2x-11)^2020=(2x-11)^202
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 3 2019
Xét cấp số cộng 1, 6, 11, ..., 96.
Ta có: 96 = 1 + 5(n − 1) ⇒ n = 20
Suy ra
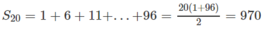
Và 2x.20 + 970 = 1010
Từ đó x = 1
6 tháng 10 2021
\(\Rightarrow\left(\dfrac{33}{11}\right)^{2x}=81\Rightarrow3^{2x}=3^4\Rightarrow x=2\)
28 tháng 10 2020
( 2x - 3 )x + 2020 - ( 2x - 3 )x + 20 = 0
=> ( 2x - 3 )x + 20 . [( 2x - 3 )2000 - 1 ] = 0
=> 2x - 3 = 0 2x = 3 x = 3/2
hoặc => =>
2x - 3 = 1 2x = 4 x = 2
b, ( 3x - 1 )n + 1 = ( 3x - 1 )n + 11
=> ( 3x - 1 )n + 11 - ( 3x - 1 )n + 1 = 0
=> ( 3x - 1 )n + 1 . [( 3x - 1 )10 - 1 ] = 0
=> 3x - 1 = 0 3x = 1 x = 1/3
hoặc => =>
3x - 1 = 1 3x = 2 x = 2/3
28 tháng 10 2020
\(\left(2x-3\right)^{x+2020}-\left(2x-3\right)^{x+20}=0\)
\(\Leftrightarrow\left(2x-3\right)^{x+20}\left[\left(2x-3\right)-1\right]=0\)
\(\Leftrightarrow\left(2x-3\right)^{x+2020}\left(2x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=2\end{cases}}\)
NT
0
LT
1
25 tháng 4 2015
Ta có:
(9/2 - 2X) . 11/3 = 11/15
9/2 - 2X = 11/15 : 11/3
9/2 - 2X = 1/5
2X = 9/2 - 1/5
2X = 4,3(hoặc 43/10)
X = 4,3 : 2 (hoặc 43/10 : 2)
X = 2,15
P/S : Đã kiểm chứng bằng máy tính
TU
1
17 tháng 3 2020
2x-(25-4)=11-(15+11)
2x-21=11-26
2x-21=11+(-26)
2x-21=-15
2x=(-15)+21
2x=6
x=6:2
x=3
Chúc bạn hok tốt, bạn nhớ k cho mik nha!!!!!!!
22 tháng 7 2019
b) \(x^3+6x^2+9x=0\)
\(\Leftrightarrow x^3+3x^2+3x^2+9x=0\)
\(\Leftrightarrow x^2\left(x+3\right)+3x\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2+3x\right)=0\)
\(\Leftrightarrow\left(x+3\right)x\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)^2x=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+3\right)^2=0\\x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=0\end{cases}}}\)
Vậy \(x\in\left\{-3;0\right\}\)
22 tháng 7 2019
a) \(2x\left(x-2\right)+x^2=4\)
\(\Leftrightarrow2x\left(x-2\right)+x^2-4=0\)
\(\Leftrightarrow2x\left(x-2\right)+\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x+x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\3x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=\frac{-2}{3}\end{cases}}}\)
Vậy \(x\in\left\{\frac{-2}{3};2\right\}\)
12 tháng 2 2021
1 Tìm số nguyên x bik:
a.-( 2x+2)+25=-19
-2x - 2 + 25 = - 19
-2x = -19+2-25
-2x = -42
x = 21
b.1-(12+3x)=7
1 - 12 - 3x = 7
- 11 - 3x = 7
-3x = 7 + 11
- 3x = 18
x = -6
c.-(2x+2)+25=-19
giống câu a nhé
2.Rút gọn biểu thức
a.2x+(-61)-(21-61)
= 2x - 61 - 21 + 61
= 2x - 21
b. (-3-x+5)+3
= 2 - x + 3
= -1 -x
c.11-(13-x)+(13-11)
= 11 - 13 + x + 13 - 11
= x
d.25-(15-x+303)+303
= 25 - 15 + x - 303 + 303
= 10 + x
e.x+(-81)-(11-8)
= x - 81 - 11 + 8
= x - 84
f. (-1-x+2)+1
= -1 - x + 2 + 1
= - x + 2
g.15-(11-x)+(11-15)
= 15 - 11 + x + 11 - 15
= x
i) 15-(15-x+202)+202
= 15 - 15 + x - 202 + 202
= x
3.Chứng minh đẳng thức
a.-(59-3x)+39=3x-20
- 59 + 3x + 39 = 3x - 20
- 59 + 39 + 20 = 3x - 3x
0 = 0
b.-(a+b+c)+(b-c)-(a-c-1)=1+c-29
b - a - b - c + b - c - a + c + 1 = 1 + c - 29
b - a - b - c + b - c - a + c - c = 1 - 29 - 1
- 2a + b - 2c = - 29
chịu luôn -__-
c.-(19-2x)+39=2x+20
- 19 + 2x + 39 = 2x + 20
2x - 2x = 20 + 19 - 29
0 = 0
d.-(a+b+c)+b-c-( a-c+1)=c-2a-1
- a - b - c + b - c - a + c - 1 = c - 2a - 1
- a - b - c + b - c - a + c + 2a - c = -1 + 1
- 2c = 0
c = 0
Vậy c = 0
`(2x-11)^2020=(2x-11)^202`
`=>(2x-11)^2020:(2x-11)^202=(2x-11)^202:(2x-11)^202`
`=>(2x-11)^1818=1`
`=>2x-11=1`
`=>2x=12`
`=>x=6`
\(\left(2x-11\right)^{2020}=\left(2x-11\right)^{202}\)
\(\Leftrightarrow\left(2x-11\right)^{2020}-\left(2x-11\right)^{202}=0\)
\(\Leftrightarrow\left(2x-11\right)^{202}.\left[\left(2x-11\right)^{1818}-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x-11\right)^{202}=0\\\left(2x-11\right)^{1818}-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-11=0\\\left(2x-11\right)^{1818}=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-11=0\\\left[{}\begin{matrix}\left(2x-11\right)^{1818}=1^{1818}\\\left(2x-11\right)^{1818}=\left(-1\right)^{1818}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=11\\2x-11=1\\2x-11=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{2}\\x=6\\x=5\end{matrix}\right.\)