1. tìm x nguyên để phân thức sau nhận gtri nguyên (x + 2)/(x^2 + 4)
2. tìm gtln của 6x - 8 / x^2 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MA
31 tháng 12 2017
1) Ta có:
x³ + y³ + z³ - 3xyz = (x+y)³ - 3xy(x-y) + z³ - 3xyz
= [(x+y)³ + z³] - 3xy(x+y+z)
= (x+y+z)³ - 3z(x+y)(x+y+z) - 3xy(x-y-z)
= (x+y+z)[(x+y+z)² - 3z(x+y) - 3xy]
= (x+y+z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy)
= (x+y+z)(x² + y² + z² - xy - xz - yz).
LD
31 tháng 12 2017
Câu 2:
\(\frac{x^2-y^2+6x+9}{x+y+3}\)
\(=\frac{x^2-y^2+x^2+6x+9-x^2}{x+y+3}\)
\(=\frac{ \left(x+3\right)^2-y^2}{x+y+3}\)
\(=\frac{\left(x-y+3\right)\left(x+y+3\right)}{x+y+3}\)
\(=x-y+3\)
27 tháng 10 2021
Bài 1:
a: \(Q=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\left(x+\sqrt{x}\right)\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\left(\sqrt{x}+1\right)\)
\(=\dfrac{2x}{x-1}\)
18 tháng 11 2017
MK ko biế đúng ko nữa , sai thì ý kiến
a)
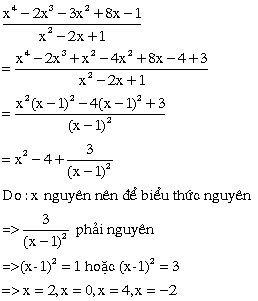
b)
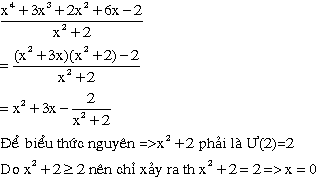
Chúc các bn hok tốt
Tham khảo nhé
3 tháng 4 2021
a, \(B=\left(\frac{9-3x}{x^2+4x-5}-\frac{x+5}{1-x}-\frac{x+1}{x+5}\right):\frac{7x-14}{x^2-1}\)
\(=\left(\frac{9-3x}{\left(x-1\right)\left(x+5\right)}+\frac{\left(x+5\right)^2}{\left(x-1\right)\left(x+5\right)}-\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+5\right)}\right):\frac{7\left(x-2\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{9-3x+x^2+10x+25-x^2+1}{\left(x-1\right)\left(x+5\right)}.\frac{\left(x-1\right)\left(x+1\right)}{7\left(x-2\right)}\)
\(=\frac{35+7x}{x+5}\frac{x+1}{7\left(x-2\right)}=\frac{7\left(x+5\right)\left(x+1\right)}{7\left(x+5\right)\left(x-2\right)}=\frac{x+1}{x-2}\)
b, Ta có : \(\left(x+5\right)^2-9x-45=0\)
\(\Leftrightarrow x^2+10x+25-9x-45=0\Leftrightarrow x^2+x-20=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x=4\\x=5\end{cases}}\)
TH1 : Thay x = 4 vào biểu thức ta được : \(\frac{4+1}{4-2}=\frac{5}{2}\)
TH2 : THay x = 5 vào biểu thức ta được : \(\frac{5+1}{5-2}=\frac{6}{3}=2\)
c, Để B nhận giá trị nguyên khi \(\frac{x+1}{x-2}\inℤ\Rightarrow x-2+3⋮x-2\)
\(\Leftrightarrow3⋮x-2\Rightarrow x-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| x - 2 | 1 | -1 | 3 | -3 |
| x | 3 | 1 | 5 | -1 |
3 tháng 4 2021
d, Ta có : \(B=-\frac{3}{4}\Rightarrow\frac{x+1}{x-2}=-\frac{3}{4}\)ĐK : \(x\ne2\)
\(\Rightarrow4x+4=-3x+6\Leftrightarrow7x=2\Leftrightarrow x=\frac{2}{7}\)( tmđk )
e, Ta có B < 0 hay \(\frac{x+1}{x-2}< 0\)
TH1 : \(\hept{\begin{cases}x+1< 0\\x-2>0\end{cases}\Rightarrow\hept{\begin{cases}x< -1\\x>2\end{cases}}}\)( ktm )
TH2 : \(\hept{\begin{cases}x+1>0\\x-2< 0\end{cases}}\Rightarrow\hept{\begin{cases}x>-1\\x< 2\end{cases}\Rightarrow-1< x< 2}\)
16 tháng 9 2018
1 Giải :
\(\frac{3x+7}{x-1}\)là phân số <=> x - 1 \(\ne\)0 => x \(\ne\)1
Ta có : \(\frac{3x+7}{x-1}=\frac{3\left(x-1\right)+8}{x-1}=3+\frac{8}{x-1}\)
Để \(\frac{3x+7}{x-1}\)là số nguyên thì 8 \(⋮\)x - 1 => x - 1 \(\in\)Ư(1; -1; 2; -2; 4; -4; 8; -8}
Lập bảng :
| x - 1 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| x | 2 | 0 | 3 | -1 | 5 | -3 | 9 | -7 |
Vậy x \(\in\){2; 0; 3; -1; 5; -3; 9; -7} thì \(\frac{3x+7}{x-1}\)là số nguyên
D
16 tháng 9 2018
Đặt \(A=\frac{3x+7}{x-1}\)
Ta có: \(A=\frac{3x+7}{x-1}=\frac{3x-3+10}{x-1}=\frac{3x-3}{x-1}+\frac{10}{x-1}=3+\frac{10}{x-1}\)
Để \(A\in Z\)thì \(\frac{10}{x-1}\in Z\Rightarrow10⋮x-1\Leftrightarrow x-1\in U\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Ta có bảng sau:
| \(x-1\) | \(1\) | \(-1\) | \(2\) | \(-2\) | \(5\) | \(-5\) | \(10\) | \(-10\) |
| \(x\) | \(2\) | \(0\) | \(3\) | \(-1\) | \(6\) | \(-4\) | \(11\) | \(-9\) |
Vậy, với \(x\in\left\{-9;-4;-1;0;2;3;6;11\right\}\)thì \(A=\frac{3x+7}{x-1}\in Z\)
1 tháng 2 2022
a: \(M=\left(\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{6}{3\left(x-2\right)}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(=\left(\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x-2}+\dfrac{1}{x+2}\right):\dfrac{x^2-4+10-x^2}{x+2}\)
\(=\dfrac{x-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}\)
\(=\dfrac{-1}{x-2}\)
b: Để M đạt giá trị lớn nhất thì x-2=-1
hay x=1
c: Để M=3x thì \(\dfrac{-1}{x-2}=3x\)
\(\Leftrightarrow3x^2-6x+1=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot3\cdot1=36-12=24\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{6-2\sqrt{6}}{6}=\dfrac{3-\sqrt{6}}{3}\\x_2=\dfrac{3+\sqrt{6}}{3}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
\(C=\dfrac{\left(x^2+3x\right)\left(x^2+2\right)-2}{x^2+2}=x^2+3x-\dfrac{2}{x^2+2}\)
\(C\in Z\Leftrightarrow2⋮\left(x^2+2\right)\)
\(\Leftrightarrow x^2+2=2\Rightarrow x=0\)
\(\frac{x+2}{x^2+4}\in Z\Rightarrow x+2⋮x^2+4\)
\(\Rightarrow\left(x+2\right)\left(x-2\right)⋮x^2+4\)
\(\Rightarrow x^2-4⋮x^2+4\)
Mà \(x^2+4⋮x^2+4\)
\(\Rightarrow\left(x^2+4\right)-\left(x^2-4\right)⋮x^2+4\)
\(\Rightarrow8⋮x^2+4\)
\(\Rightarrow x^2+4\inƯ\left(8\right)\)
Mà \(x^2+4\ge0+4=4\Rightarrow x^2+4\in\left\{4;8\right\}\)
\(\Rightarrow x^2\in\left\{0;4\right\}\)
\(\Rightarrow x\in\left\{-2;0;2\right\}\)
Với \(x=-2\Rightarrow\frac{x+2}{x^2+4}=\frac{0}{4+4}=0\in Z\left(TM\right)\)
Với \(x=0\Rightarrow\frac{x+2}{x^2+4}=\frac{2}{0+4}=\frac{1}{2}\notin Z\left(0TM\right)\)
Với \(x=2\Rightarrow\frac{x+2}{x^2+4}=\frac{4}{4+4}=\frac{1}{2}\notin Z\left(0TM\right)\)
Do đó \(x=-2\)
Vậy ...