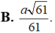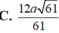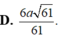cho hình vuông abcd có ab =6 cmgọi M,N,Plần lượt là trg điểm BD ,MD,CB tính góc ANP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2021
a: Xét ΔAHB có
M là trung điểm của HA
N là trung điểm của HB
Do đó: MN là đường trung bình của ΔAHB
Suy ra: MN//DP và MN=DP
hay DMNP là hình bình hành
CM
15 tháng 4 2017
Đáp án B
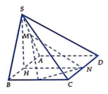
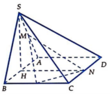
Gọi H là trung điểm của cạnh AB. Khi đó S H ⊥ ( A B C D )
Ta có S H ⊥ A B ; A B ⊥ H N ; H N ⊥ S H và S H = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:
B ( 1 ; 0 ; 0 ) ; A ( - 1 ; 0 ; 0 ) ; N ( 0 ; 2 3 ; 0 ) ; C ( 1 ; 2 3 ; 0 ) ; D ( - 1 ; 2 3 ; 0 ) ; S ( 0 ; 0 ; 3 ) ; M ( - 1 2 ; 0 ; 3 2 ) ; P ( 1 ; 3 ; 0 )
Mặt phẳng (SCD) nhận n 1 → = - 3 6 C D → , S C → = 0 ; 1 ; 2 làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận n 2 → = - 2 3 3 M N → , M P → = 3 ; 1 ; 5 làm một vectơ pháp tuyến.
Gọi ∅ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
cos ∅ = n 1 → . n 2 → n 1 → . n 2 → = 11 145 145
CM
1 tháng 6 2017
Đáp án C
Rễ thấy Δ C D N = Δ D A M ⇒ D C N ^ = A D M ^
mà C D H ^ + M D H ^ = 90 0 ⇒ C D H ^ + D C H ^ = 90 0 ⇒ C H ⊥ D H
mà C H ⊥ S H do S H ⊥ A B C D ⇒ D H ⊥ S C H .
Như vậy kẻ H K ⊥ S C thì HK là đường vuông góc chung của DM và SC hay HK là khoảng cách cần xác định.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
C D 2 = C H . C N ⇒ C H = C D 2 C N = C D 2 C D 2 + D N 2 = 4 a 2 4 a 2 + a 2 = 2 a 5
1 H K 2 = 1 S H 2 + 1 C H 2 = 1 9 a 2 + 5 16 s 2 = 61 144 a 2 ⇒ H K = 12 a 61 61
4 tháng 2 2022
Bài 1:
Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ=NP và MQ//NP
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN=AC/2=BD/2(3)
Từ (1) và (3) suy ra MQ=MN
Xét tứ giác MQPN có
MQ//PN
MQ=PN
Do đó: MQPN là hình bình hành
mà MQ=MN
nên MQPN là hình thoi
Suy ra: MP⊥NQ
15 tháng 8 2021
b: Ta có: \(AE=ED=\dfrac{1}{2}AD\)
mà \(AB=BC=\dfrac{AD}{2}\)
nên AE=ED=AB=BC
Xét tứ giác AECB có
AE//CB
AE=CB
Do đó: AECB là hình bình hành
mà \(\widehat{EAB}=90^0\)
nên AECB là hình chữ nhật
mà AE=AB
nên AECB là hình vuông
Xét ΔHAD có
N là trung điểm của AH
M là trung điểm của HD
Do đó: MN là đường trung bình của ΔHAD
Suy ra: MN//AD và \(MN=\dfrac{AD}{2}\)
mà \(AE=BC=\dfrac{AD}{2}\) và AD//BC
nên MN//BC và MN=BC
Xét tứ giác BCMN có
MN//BC
MN=BC
Do đó: BCMN là hình bình hành