giúp mình trả lời với vẽ hình đc k ạ, hicc mình cảm ơn nhiều😢
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Q
2
Những câu hỏi liên quan
HT
6 tháng 1 2021
Okie, xinh nên giúp :3 Đùa thui
a/ 5 nguồn mắc nối tiếp \(\left\{{}\begin{matrix}\xi_b=5.\xi=5.4=20\left(V\right)\\r_b=5r=5.0,2=1\left(\Omega\right)\end{matrix}\right.\)
b/ \(R_D=\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{36}{6}=6\left(\Omega\right);I_{dm}=\dfrac{P_{dm}}{U_{dm}}=\dfrac{6}{6}=1\left(A\right)\)
Đèn sáng bình thường \(\Rightarrow I_2=I_D=I_{dm}=1\left(A\right)\)
\(\left(R_1ntR_B\right)//\left(R_2ntR_D\right)\Rightarrow R_{td}=\dfrac{\left(R_1+R_B\right)\left(R_2+R_D\right)}{R_1+R_B+R_2+R_D}=\dfrac{\left(2+4\right)\left(6+6\right)}{2+4+6+6}=4\left(\Omega\right)\)
c/ \(I=\dfrac{\xi_b}{r_b+R_{td}}=\dfrac{20}{1+4}=4\left(A\right)\)
\(I=I_1+I_2\Rightarrow I_1=I-I_2=4-1=3\left(A\right)\Rightarrow P_1=I_1^2.R_1=3^2.2=18\left(W\right)\)
\(m_{Cu}=\dfrac{A_{Cu}.I_B.t}{F.n}=\dfrac{64.3.\left(32.60+10\right)}{96500.2}=...\left(g\right)\)
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
TC
7 tháng 2 2020
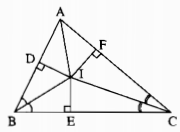
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
H
7 tháng 2 2020
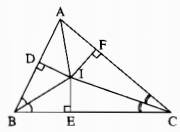
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
18 tháng 7 2021
_ Trích mẫu thử.
_ Hòa tan vào nước và thả quỳ tím vào.
+ Nếu không tan, đó là MgO.
+ Nếu tan, làm quỳ chuyển đỏ, đó là P2O5.
PT: \(P_2O_5+3H_2O\rightarrow2H_3PO_4\)
+ Nếu tan, làm quỳ chuyển xanh, đó là CaO, Na2O (1)
PT: \(CaO+H_2O\rightarrow Ca\left(OH\right)_2\)
\(Na_2O+H_2O\rightarrow2NaOH\)
_ Sục khí CO2 vào dd thu được ở nhóm (1).
+ Nếu xuất hiện kết tủa trắng, đó là CaO.
PT: \(Ca\left(OH\right)_2+CO_2\rightarrow CaCO_{3\downarrow}+H_2O\)
+ Nếu không hiện tượng, đó là Na2O.
PT: \(2NaOH+CO_2\rightarrow Na_2CO_3+H_2O\)
_ Dán nhãn.
Bạn tham khảo nhé!
18 tháng 7 2021
- Trích mỗi chất một ít làm mẫu thử đồng thời đánh số thứ tự (1),(2),(3),(4) ở các ống nghiệm và các lọ chứa hóa chất tương ứng.
- Dùng nước làm thuốc thử đầu tiên:
+ Không tan -> MgO
+ Còn lại đều tan, tạo thành dung dịch.
PTHH: Na2O + H2O -> 2 NaOH
CaO + H2O -> Ca(OH)2
P2O5 +3 H2O -> 2 H3PO4
- Dùng quỳ tím cho vào 3 dung dịch vừa được tạo ra:
+ Qùy tím hóa đỏ -> dd H3PO4 => Nhận biết P2O5.
+ Qùy tím hóa xanh -> dd NaOH, dd Ca(OH)2
- Dẫn khí CO2 vào 2 dung dịch chưa nhận biết được, quan sát thấy:
+ Xuất hiện kt trắng -> CaCO3 -> dd Ca(OH)2 => Nhận biết CaO
+ Không có kết tủa trắng -> dd NaOH => Na2O
PTHH: Ca(OH)2 + CO2 -> CaCO3 (kt trắng) + H2O
2 NaOH + CO2 -> Na2CO3 + H2O
12 tháng 1 2022
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
b: Xét ΔAIH vuông tại I và ΔAKH vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAIH=ΔAKH
Suy ra: AI=AK
c: Xét ΔABC có
AI/AB=AK/AC
Do đó: IK//BC
WY
0
TT
21 tháng 2 2020
Ta có : \(12a+7b=64\)
Do \(64⋮4,12a⋮4\) \(\Rightarrow7b⋮4\) mà \(\left(7,4\right)=1\)
\(\Rightarrow b⋮4\) (1)
Từ giả thiết \(\Rightarrow7b\le64\) \(\Leftrightarrow b\le9\) kết hợp với (1)
\(\Rightarrow b\in\left\{4,8\right\}\)
+) Với \(b=4\) thì : \(12a+7\cdot4=64\)
\(\Leftrightarrow12a=36\)
\(\Leftrightarrow a=3\) ( thỏa mãn )
+) Với \(b=8\) thì \(12a+7\cdot8=64\)
\(\Leftrightarrow12a=8\)
\(\Leftrightarrow a=\frac{8}{12}\) ( loại )
Vậy : \(\left(a,b\right)=\left(3,4\right)\)
Vẽ hình giúp mình với nhé cảm ơn nhiều ạ
15 tháng 10 2023
6:
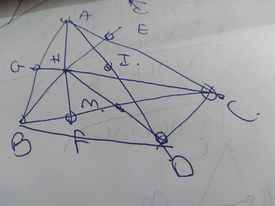
a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
nên BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CD và CH//BD
BH//CD
BH vuông góc AC
Do đó: CD vuông góc AC
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc BA
=>ΔABD vuông tại B
c: Xét tứ giác ABDC có
\(\widehat{ABD}+\widehat{ACD}=90^0+90^0=180^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=IC=ID
a: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
b: Ta có: ΔBAK=ΔBDK
nên KA=KD
mà BA=BD
nên BK là đường trung trực của AD
A B C D O K
a)Xét \(\Delta BAK\) và \(\Delta BDK\) có:
AB=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
=> \(\Delta BAK\) = \(\Delta BDK\) (c-g-c)
b)Gọi O là giao điểm của AD và BK
Xét \(\Delta ABO\) và \(\Delta DBO\) có :
BO chung
\(\widehat{ABO}=\widehat{DBO}\)
AB=DB
=> \(\Delta ABO\) và \(\Delta DBO\) (c-g-c)
=> AO=BO (1) ; \(\widehat{AOB}=\widehat{DOB}\)
Có : \(\widehat{AOB}+\widehat{DOB}=180^o\) mà \(\widehat{AOB}=\widehat{DOB}\)
=> \(\widehat{AOB}=\widehat{DOB}=\dfrac{180^o}{2}=90^o\) (2)
Từ (1)(2) => BK là đường trung trực cùa AD