43 - 2x2 = 14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 2 2019
Ta thấy:
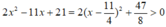
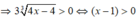
Áp dụng bất đẳng thức Cô – si ta có:
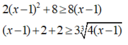
Cộng vế với vế ta được:
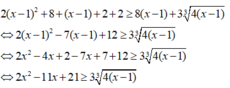
Dấu “=” xảy ra khi và chỉ khi x - 1 = 2 ⇔ x = 3
Vậy x = 3 là nghiệm của phương trình.
CM
26 tháng 9 2019
Ta có f (a) = −8 + 4 3 −2a2 = −8 + 4 3
⇔ a2 = 4 − 2 3 ⇔ a2 = ( 3 − 1)2
⇔ a = 3 − 1 a = 1 − 3
Vậy tổng các giá trị của a là:( 3 − 1) + (1 − 3 ) = 0
Đáp án cần chọn là: B
CM
1 tháng 9 2018
Đáp án B
Thay a vào hàm số y = f ( x ) = - 2 x 2 . ta được:
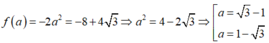
Tổng các giá trị của a là: 3 - 1 + 1 - 3 = 0
CM
25 tháng 4 2019
Đáp án B
Phương pháp:
- Chia cả hai vế của phương trình cho x + 1 > 0 và đặt ẩn phụ t = x − 1 4 x + 1 4 .
- Từ điều kiện x ≥ 1 ta tìm được điều kiện của t là 0 ≤ t < 1 .
- Từ phương trình ẩn t, rút − m = f t và xét hàm f t trên 0 ; 1 , từ đó suy ra điều kiện của
Cách giải:
Phương trình: 3 x − 1 + m x + 1 = 2 x 2 − 1 4 (Điều kiện: x ≥ 1 )
3 x − 1 + m x + 1 = 2 x − 1 4 . x + 1 4 *
Ta có với x ≥ 1 Chia hai vế phương trình (*) cho ta có: 3 x − 1 x + 1 + m = 2 x − 1 4 x + 1 4 1
Đặt t = x − 1 4 x + 1 4 ⇒ t 4 = x − 1 x + 1
Với x ≥ 1 thì hàm số 0 ≤ x − 1 x + 1 = 1 − 2 x + 1 < 1 ⇒ 0 ≤ t 4 < 1 ⇔ 0 ≤ t < 1
Phương trình (1) trở thành: 3 t 2 − 2 t + m = 0 2
Phương trình (*) có nghiệm phương trình (2) có nghiệm: 0 ≤ t < 1
Xét hàm y = f t = 3 t 2 − 2 t trên 0 ; 1 ta có:
f ' t = 6 t − 2 = 0 ⇔ t = 1 3 ∈ 0 ; 1
Bảng biến thiên:
Từ bảng biến thiên ta thấy để phương trình 3 t 2 − 2 t + m = 0 có nghiệm trong 0 ; 1 thì đường thẳng y = − m phải cắt đồ thị hàm số y = f t = 3 t 2 − 2 t tại ít nhất 1 điểm.
Do đó − 1 3 ≤ − m < 1 ⇔ − 1 < m ≤ 1 3
Vậy − 1 < m ≤ 1 3 thì phương trình đã cho có nghiệm.
Đáp án B.
Chú ý khi giải:
- HS thường quên không tìm điều kiện của ẩn phụ hoặc tìm sai điều kiện (một số bạn chỉ đặt điều kiện sẽ dẫn đến kết quả sai) t t 0
- Ở bước kết luận, một số bạn nhầm lẫn điều kiện để có nghiệm và có 2 nghiệm nên sẽ chọn để phương trình có 2 nghiệm cũng là một kết quả sai. 1 0 m 3
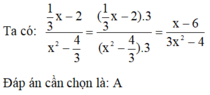
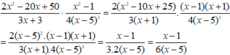
43- 2x2= 14
=>2x2= 29
=>x2=29/2=\(\left(\sqrt{\frac{29}{2}}\right)^2\)
=>x=\(\sqrt{\frac{29}{2}}\)hoặc x=\(-\sqrt{\frac{29}{2}}\)