Cho tam giác ABC có AB=AC, AH là đường trung tuyến. Cho biết AB=29cm, BC=40cm. Tính AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
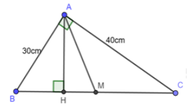
Cho tam giác ABC có Â tù. Từ A kẻ AH vuông góc BC. Biết AB=29cm, AC= 40cm, AH= 1/2 BC. Tính BH và HC
3
11 tháng 1 2022
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
29 tháng 2 2024
- có = 900, AM là trung tuyến MB = MC = 41
- Tính được: HM = 9 (cm), HB = 32 (cm); HC = 50 (cm)
- Xét vuông tại H AB2 = BH2 + AH2 = 322 + 402 = 2624
- Xét vuông tại H AC2 = AH2 + HC2 = 402 + 502 = 4100
- Suy ra: =
DK
1
CM
19 tháng 9 2019
Áp dụng định lý Pytago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
Vì AM là đường trung tuyến M là trung điểm BC
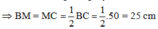
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A
11 tháng 9 2016
BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!
tam giác ABC có AB=AC,
=> tam giác ABC cân tại A
lại có AH là đường trung tuyến
nên AH đồng thời là đg cao (AH⊥BC)
\(=>BH=CH=\dfrac{1}{2}BC=20\left(cm\right)\)
xét tam giác ABH vuông tại H ta có
\(AB^2=AH^2+BH^2\)
\(=>AH=\sqrt{AB^2-BH^2}=\sqrt{29^2-20^2}=21\cdot cm\)
Ta có AH là đường trung tuyến
=> BH = BC/2 = 20 cm
Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-AH^2}=21cm\)