cho tam giác abc vuông cân tại a, điểm m thuộc cạnh bc có ma = a. tính tổng mb^2+mc^2 theo a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tính đối xứng, không mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow BH=CH=AH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(BH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(BH^2+MH^2\right)}=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)

Do tính đối xứng, ko mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow AH\) đồng thời là trung tuyến
\(\Rightarrow AH=\dfrac{1}{2}BC\Rightarrow AH=BH=CH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-HM\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(AH-MH\right)^2+\left(AH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)



Do MA và MC không đổi =>Để AM^2+BM^2+CM^2 nhỏ nhất =>AM là đường cao của tam giác ABC (1)
Mà ABC vuông cân =>M là trung điểm của BC
Kẻ MI vuông góc với AB,MK vuông góc với AC
suy ra MI // Ak,AI // MK suy ra AIMK là hình chữ nhật
Ta có :AM^2+BM^2+CM^
=AI^2+IM^2+IM^2+IB^2+CK^2+MK^2
=2AI^2+2IM^2+AM^2
=2*(AI^2+IM^2)+AM^2
=3AM^2
Từ (1) => AM^2+BM^2+c

Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK
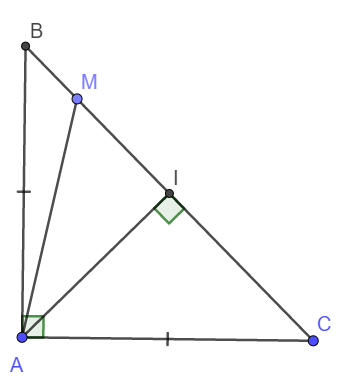
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.
\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)
Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )
Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)
\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)
\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)
\(=2AM^2\)
Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)
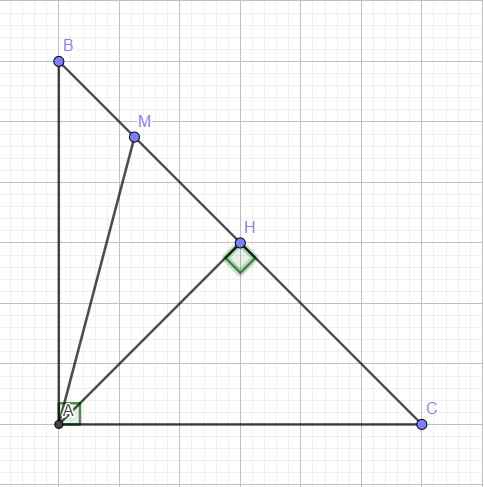
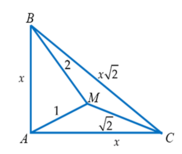


Từ B kẻ đường thẳng vuông góc với BC tại B cắt AC tại M
=> BK là đường cao tg vuông CBM
=> 1/BK^2 = 1/BC^2 + 1/BM^2 (*)
Mặt khác AH//BC và HB=HC do tg ABC cân
=> AH là đường trung bình tg CBM
=> BM =2AH
Do đó từ (*) => 1/BK^2 = 1/BC^2 + 1/4AH^2
2]
Từ M kẻ MP _|_AB; MQ _|_AC
Do ^ABC = ^ACB =45o
=> tg MPQ và MQC vuông cân
=> MB^2 = 2MP^2
=> MC^2 = 2MQ^2
=> MB^2 + MC^2 = 2(MP^2+MQ^2) (*)
mà APMQ là hình chữ nhật => MP^2 + MQ^2 = PQ^2 = MA^2
Do đó từ (*) => MB^2+MC^2= 2 MA^2
thankyou DIE DEVIL