x4+4x2+5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 6 2019
Đáp án B.
Ta có: y’ = 4x3 – 8x
y’’ = 12x2 – 8
y’’(0) = -8 < 0
Suy ra x = 0 là điểm cực đại
21 tháng 8 2021
1) \(\left(3x+2\right)^2-4\\ =\left(3x+2\right)^2-2^2\\ =\left(3x+2-2\right)\left(3x+2+2\right)\\ =3x.\left(3x+4\right)\)
2) \(4x^2-25y^2=\left(2x\right)^2-\left(5y\right)^2=\left(2x-5y\right)\left(2x+5y\right)\)
3) \(4x^2-49=\left(2x\right)^2-7^2=\left(2x-7\right)\left(2x+7\right)\)
4) \(8z^3+27=\left(2z\right)^3+3^3=\left(2z+3\right)\left(4z^2+6z+9\right)\)
5) \(\dfrac{9}{25}x^4-\dfrac{1}{4}=\left(\dfrac{3}{5}x^2\right)^2-\left(\dfrac{1}{2}\right)^2=\left(\dfrac{3}{5}x^2-\dfrac{1}{2}\right)\left(\dfrac{3}{5}x^2+\dfrac{1}{2}\right)\)
6) \(x^{32}-1\\ =\left(x^{16}\right)^2-1^2\\ =\left(x^{16}-1\right)\left(x^{16}+1\right)\\ =\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
21 tháng 8 2021
1: \(\left(3x+2\right)^2-4=3x\left(3x+4\right)\)
2: \(4x^2-25y^2=\left(2x-5y\right)\left(2x+5y\right)\)
3: \(4x^2-49=\left(2x-7\right)\left(2x+7\right)\)
4: \(8z^3+27=\left(2z+3\right)\left(4z^2-6z+9\right)\)
5: \(\dfrac{9}{25}x^4-\dfrac{1}{4}=\left(\dfrac{3}{5}x^2-\dfrac{1}{2}\right)\left(\dfrac{3}{5}x^2+\dfrac{1}{2}\right)\)
7 tháng 6 2021
`a)16x^2-24x+9=25`
`<=>(4x-3)^2=25`
`+)4x-3=5`
`<=>4x=8<=>x=2`
`+)4x-3=-5`
`<=>4x=-2`
`<=>x=-1/2`
`b)x^2+10x+9=0`
`<=>x^2+x+9x+9=0`
`<=>x(x+1)+9(x+1)=0`
`<=>(x+1)(x+9)=0`
`<=>` \(\left[ \begin{array}{l}x=-9\\x=-1\end{array} \right.\)
`c)x^2-4x-12=0`
`<=>x^2+2x-6x-12=0`
`<=>x(x+2)-6(x+2)=0`
`<=>(x+2)(x-6)=0`
`<=>` \(\left[ \begin{array}{l}x=-2\\x=6\end{array} \right.\)
7 tháng 6 2021
`d)x^2-5x-6=0`
`<=>x^2+x-6x-6=0`
`<=>x(x+1)-6(x+1)=0`
`<=>(x+1)(x-6)=0`
`<=>` \(\left[ \begin{array}{l}x=6\\x=-1\end{array} \right.\)
`e)4x^2-3x-1=0`
`<=>4x^2-4x+x-1=0`
`<=>4x(x-1)+(x-1)=0`
`<=>` \(\left[ \begin{array}{l}x=1\\x=-\dfrac14\end{array} \right.\)
`f)x^4+4x^2-5=0`
`<=>x^4-x^2+5x^2-5=0`
`<=>x^2(x^2-1)+5(x^2-1)=0`
`<=>(x^2-1)(x^2+5)=0`
Vì `x^2+5>=5>0`
`=>x^2-1=0<=>x^2=1`
`<=>` \(\left[ \begin{array}{l}x=1\\x=-1\end{array} \right.\)
CM
7 tháng 2 2018
Đáp án A
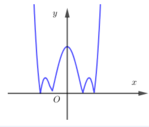
HD: Ta có: Giữ nguyên phần phía trên trục hoành, lấy đối xứng phần phía dưới trục hoành của đồ thị đã cho, ta được đồ thị hàm số y = x 4 − 4 x 2 + 3 ⇒ Hàm số có 7 cực trị.
CM
30 tháng 11 2017
Chọn đáp án B
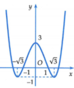
Ta có
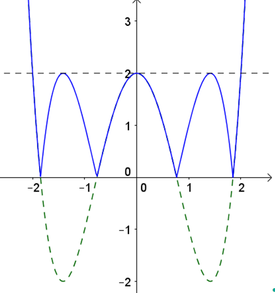
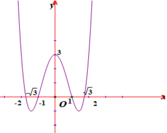
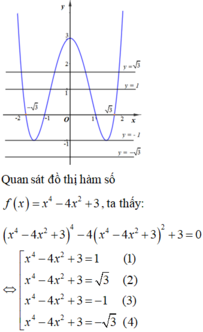
Quan sát đồ thị của hàm số y = f(x) ta thấy:
Phương trình f x = - 3 không có nghiệm; phương trình f x = - 1 có 2 nghiệm;
phương trình f x = 1 có 4 nghiệm; phương trình f x = 3 có 4 nghiệm.
Vậy phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có 10 nghiệm.
PT
1
CM
19 tháng 1 2018
Đáp án B.
Ta có
x ∈ − 2 ; 3 y ' = − 4 x 3 + 8 x = 0 ⇔ x = 0 x = ± 2
Tính
y − 2 = − 5 ; y 3 − 50 ; y 0 = − 5 ; y 2 = − 1 , y − 2 = − 1.
CM
4 tháng 1 2018
Đáp án A
f ' ( x ) = 4 x 3 − 8 x f ' ( x ) = 0 ⇔ x = 0 x = ± 2 f ( − 2 ) = 5 , f ( − 2 ) = 1 , f ( 0 ) = 5 , f ( 2 ) = 1 , f ( 3 ) = 50 G T L N [ 2 ; 3 ] f ( x ) = 50
hình như (x^2+2)^2+1
sai rồi chị ak