c)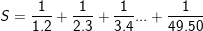 
giúp mình với, giải từng bước một
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
1
19 tháng 7 2021
a) Ta có: \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)
\(=\dfrac{1}{2}\cdot4\sqrt{3}-2\cdot5\sqrt{3}-\sqrt{3}+5\cdot\dfrac{2}{\sqrt{3}}\)
\(=-9\sqrt{3}+\dfrac{10}{\sqrt{3}}\)
\(=\dfrac{-27+10}{\sqrt{3}}=\dfrac{-17\sqrt{3}}{3}\)
4 tháng 2 2022
a) 66,8 : 89 = 0,7505...
b) 8,568 : 3,6 = 2,38
c) 429 : 572 = 0,75
d) 127 : 25,4 = 0,005
Chúc bạn học tốt.
😁😁😁
ML
2
16 tháng 9 2021
\(8,=\left(2x-3\right)\left(2x+3\right)\\ 9,=\left(1-5a^2\right)\left(1+5a^2\right)\)
16 tháng 9 2021
8) \(-9+4x^2=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
9) \(1-25a^4=1-\left(5a^2\right)^2=\left(1-5a^2\right)\left(1+5a^2\right)\)
HH
3
24 tháng 12 2022
\(\left(-2022\right)+\left(-250\right)+\left(275+2022\right)\)
\(=\left(-2022\right)-250+275+2022\)
\(=\left[\left(-2022\right)+2022\right]+\left(275-250\right)\)
\(=0+25=25\)
NT
giải từng bước giúp mình nhé
1
2 tháng 1 2022
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
NT
giải từng bước giúp mình nhé
1
2 tháng 1 2022
\(=\dfrac{2x}{x-5}+\dfrac{x}{x+5}+\dfrac{-20x}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{2x\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}+\dfrac{x\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}+\dfrac{-20x}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{2x^2+10x+x^2-5x-20x}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{3x^2-15x}{\left(x-5\right)\left(x+5\right)}\\ =\dfrac{3x}{x+5}\)
\(=>S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(S=1-\dfrac{1}{50}=\dfrac{50}{50}-\dfrac{1}{50}=\dfrac{49}{50}\)
\(S=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\)
\(S=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(S=\dfrac{1}{1}-\dfrac{1}{50}\)
\(S=\dfrac{50}{50}-\dfrac{1}{50}\)
\(S=\dfrac{49}{50}\)