Giải giúp em câu 18 với ạ em cảm ơn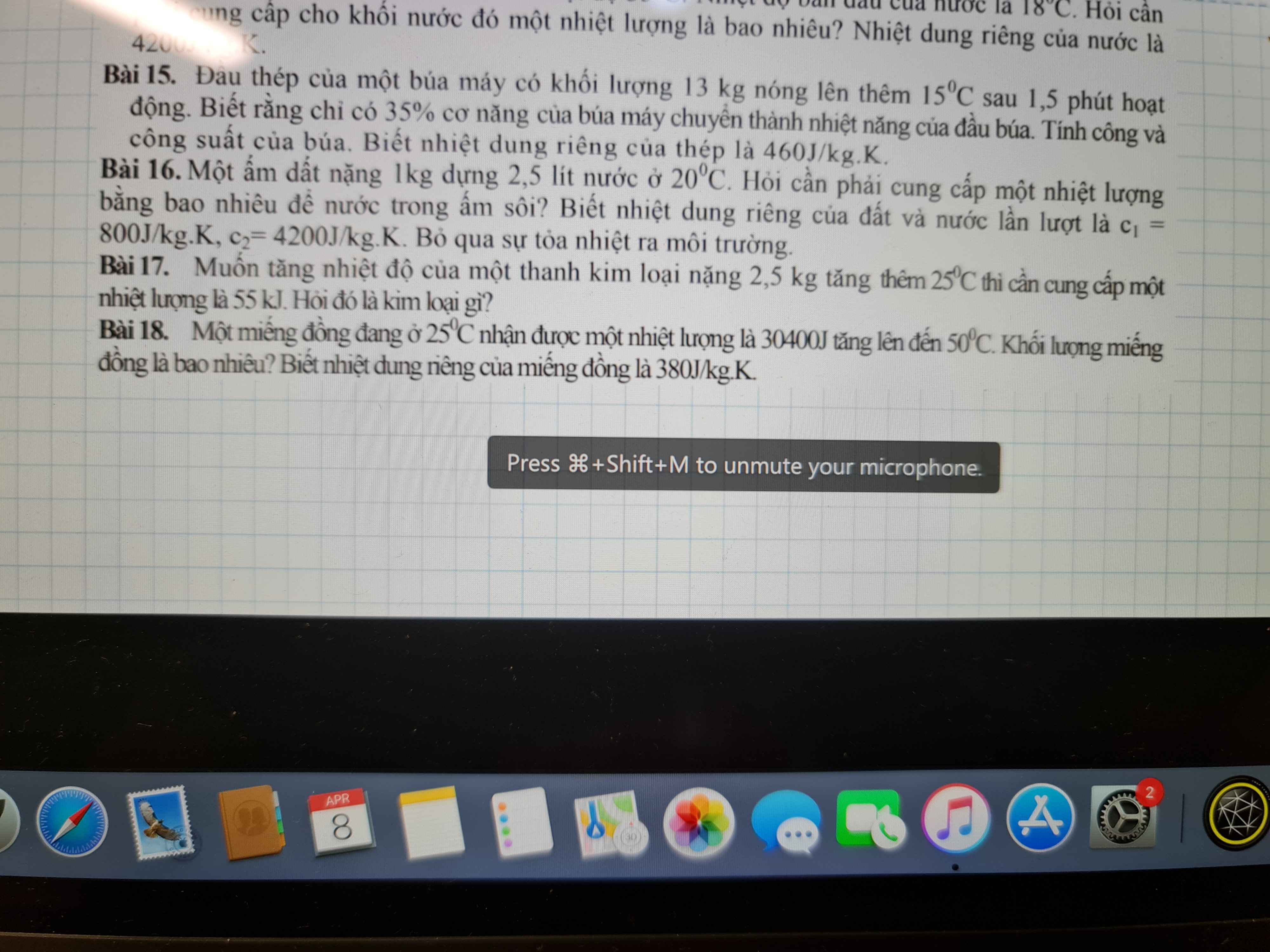
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.17+4.84−44.17+4.84-4
=4.17+4.84−4.1=4.17+4.84-4.1
=4.17+4.84−1.4=4.17+4.84-1.4
=4.(17+84−1)=4.(17+84-1)
=4.100=4.100
=400=400
_________________
17.18−18+84.1817.18-18+84.18
=17.18−18.1+84.18=17.18-18.1+84.18
=17.18+18.(−1)+84.18=17.18+18.(-1)+84.18
=18.(17−
75.12+75.9−21.2575.12+75.9-21.25
=75.(12+9)−21.25=75.(12+9)-21.25
=75.21−21.25=75.21-21.25
=75.21+21.(−25)=75.21+21.(-25)
=21.(75−25)=21.(75-25)
=21.50=21.50
=1050

Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.

Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh

1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t

2.
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=\sqrt{8^2+3^2-2.8.3.cos60^0}=7\)
\(S_{ABC}=\dfrac{1}{2}ac.sinB=\dfrac{1}{2}.8.3.sin60^0=6\sqrt{3}\)
4.
\(\Delta=\left(m+2\right)^2-16>0\Leftrightarrow m^2+4m-12>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -6\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m-2\\x_1x_2=4\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>1\)
\(\Leftrightarrow-m-2+4>1\)
\(\Rightarrow m< 1\) (2)
Kết hợp (1); (2) ta được \(m< -6\)

Gọi V là thể tích khi quay phần giới hạn bởi \(y=\dfrac{1}{x}\) ; x=1, y=0; Ox quanh Ox
\(\Rightarrow V=V_1+V_2\)
\(V=\pi\int\limits^5_1\dfrac{1}{x^2}dx=\dfrac{4\pi}{5}\)
\(V_1=\pi\int\limits^k_1\dfrac{1}{x^2}dx=-\dfrac{\pi}{x}|^k_1=\pi-\dfrac{\pi}{k}\)
\(\Rightarrow V_2=V-V_1=\dfrac{4\pi}{5}-\pi+\dfrac{\pi}{k}=\dfrac{\pi}{k}-\dfrac{\pi}{5}\)
\(\Rightarrow\pi-\dfrac{\pi}{k}=2\left(\dfrac{\pi}{k}-\dfrac{\pi}{5}\right)\)
\(\Rightarrow k=\dfrac{15}{7}\)


18) Ta có: \(H=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}+1\right)-\left(2\sqrt{x}-1\right)\)
\(=x+\sqrt{x}-2\sqrt{x}+1\)
\(=x-\sqrt{x}+1\)
19) Ta có: \(T=\dfrac{a-3\sqrt{a}-4}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}-4\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-4\)

a) 2KMnO4 +16HCl --> 2KCl + 2MnCl2 + 5Cl2 + 8H2O
Chất oxh: KMnO4; chất khử: HCl
| Mn+7 +5e->Mn+2 | x2 |
| 2Cl- -2e--> Cl20 | x5 |
b) 8Al + 30HNO3 --> 8Al(NO3)3 + 3N2O + 15H2O
| Al0 -3e --> Al+3 | x8 |
| 2N+5 +8e--> N2+1 | x3 |
31:
\(n_{Fe}=\dfrac{5,6}{56}=0,1\left(mol\right)\)
PTHH: Fe + H2SO4 --> FeSO4 + H2
_____0,1----------------->0,1
10FeSO4 + 2KMnO4 + 8H2SO4 --> K2SO4 + 2MnSO4 + 5Fe2(SO4)3 + 8H2O
=> nKMnO4 = 0,02 (mol)
=> \(V=\dfrac{0,02}{0,5}=0,04\left(l\right)=40\left(ml\right)\)







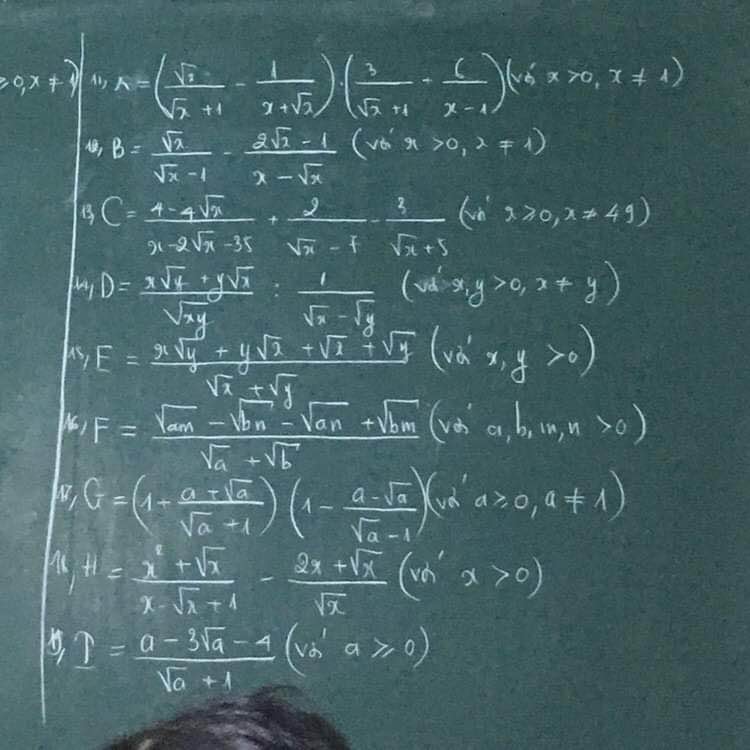

Câu 18.
Nhiệt lượng miếng đồng thu vào:
\(Q=mc\left(t_2-t_1\right)\)
\(\Rightarrow30400=m\cdot380\cdot\left(50-20\right)\)
\(\Rightarrow m=2,67kg\)