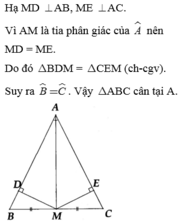
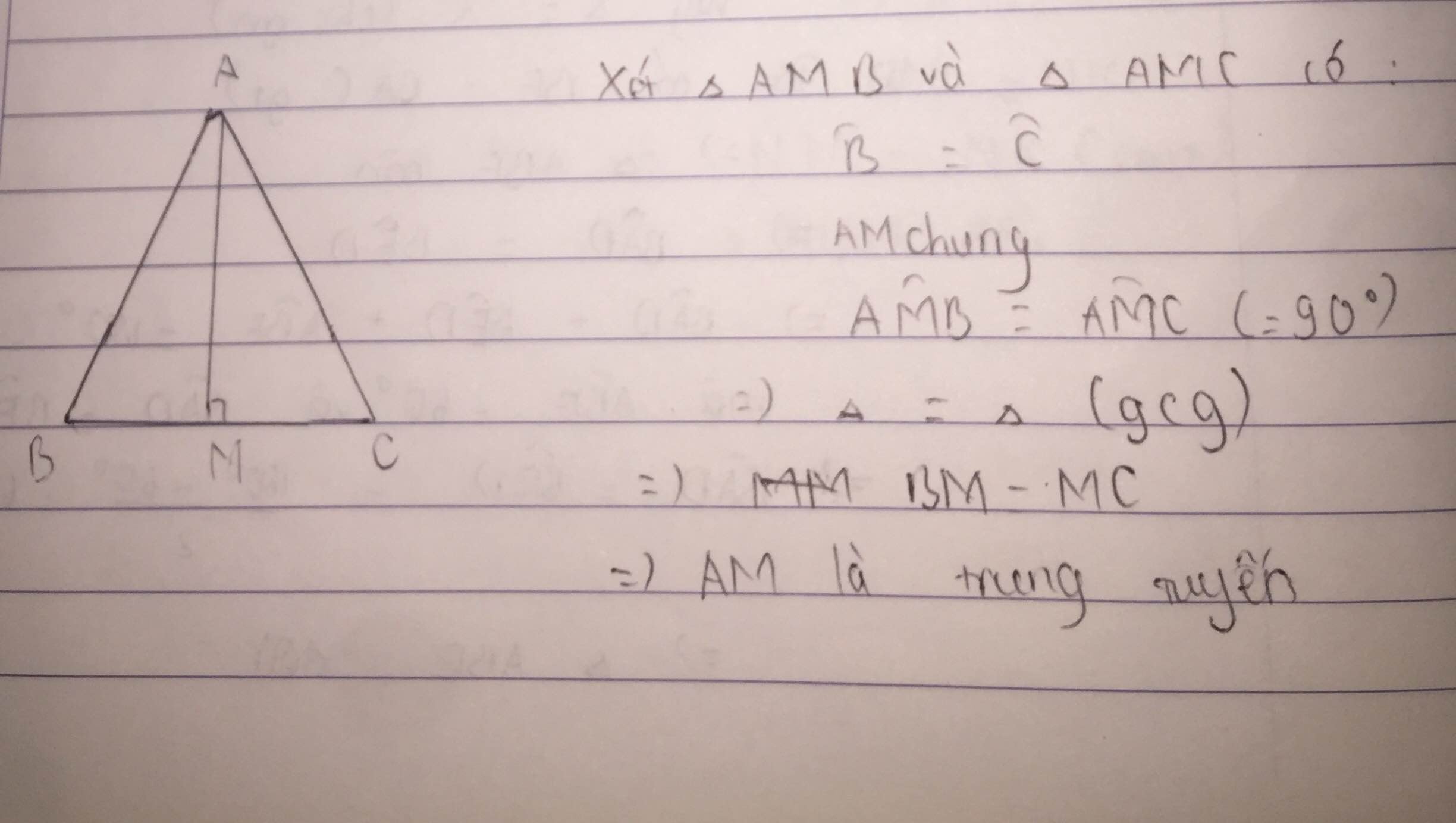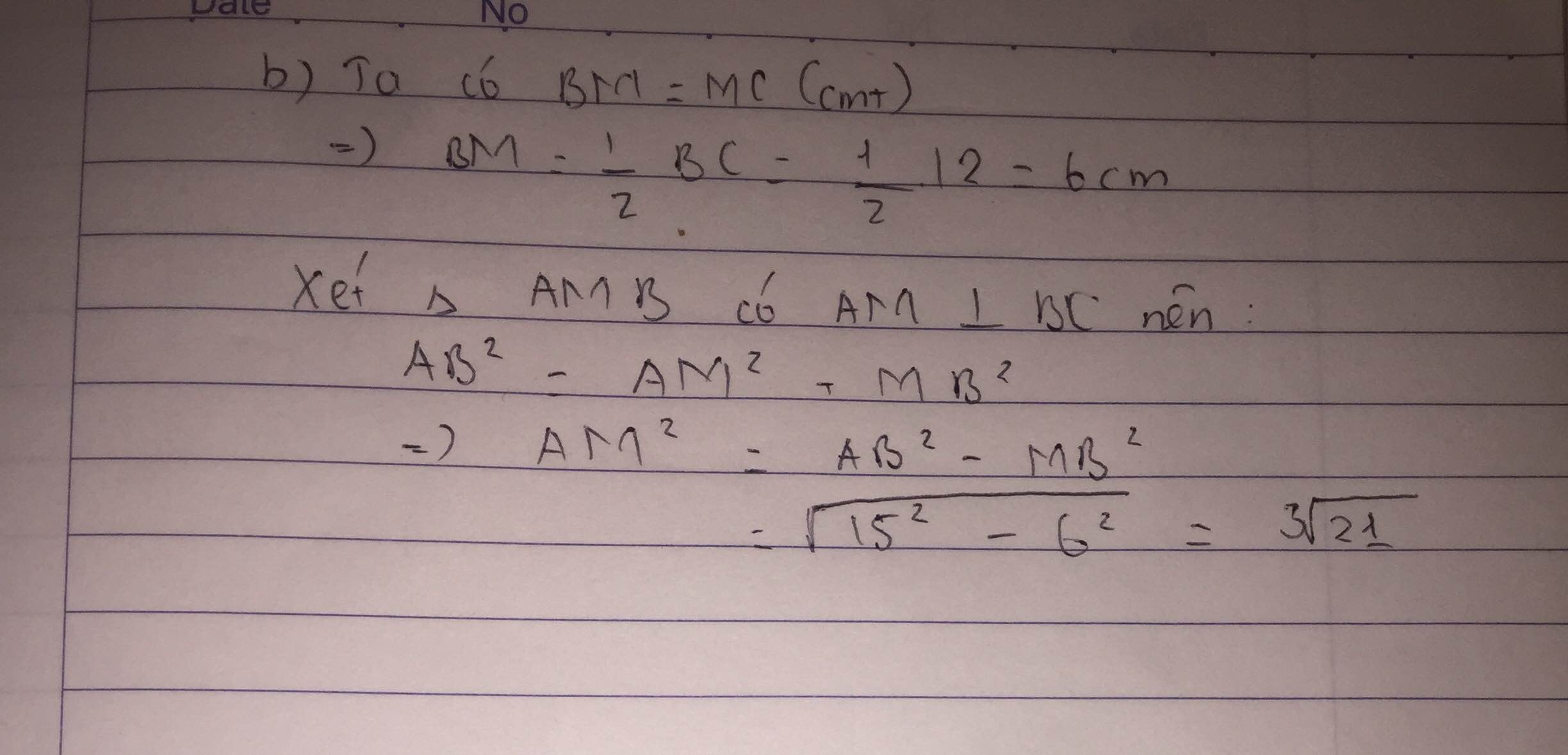Bài 1. Cho tam giác ABC cân tại A, đường trung tuyến AM; AB = 13 cm, BC = 10 cm.
a) Tính độ dài AM.
b) Trên AM lấy điểm G sao cho GM = \(\dfrac{1}{3}\) AM. Tia BG cắt AC tại N. C/m: NA = NC.
c) Tính độ dài BN.
d) Tia CG cắt AB tại L. Chứng minh rằng LN // BC.