1/2.3 + 1/3.4 + 1/4.5 + ...+1/199.200
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PP
1
CN
18 tháng 10 2017
Ta có: A=1.2+2.3+...+198.199+199.200
=>3A=1.2.3+2.3.3+...+198.199.3
+199.200.3
=>3A=1.2.3+2.3(4-1)+...+
198.199(200-197)+199.200(201-198)
=>3A=1.2.3+2.3.4-1.2.3+...+198.199.200
-197.198.199+199.200.201-198.199.200
=>3A=199.200.201
=>A=199.200.67
A=39800.67
A=2666600
NN
1
26 tháng 11 2015
3A =1.2.3 +2.3.(4-1) +3.4.(5-2) +4.5.(6-3)....+199.200.(201 -198)
= 1.2.3+2.3.4 -1.2.3 +3.4.5- 2.3.4 + 4.5.6 - 3.4.5 +......+ 199.200.201 -198.199.200
3A =199.200.201
A=199.200.67 =254600
S
20 tháng 2 2019
\(A=\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{199\cdot200}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{199}-\frac{1}{200}\)
\(A=1-\frac{1}{200}\)
\(A=\frac{199}{200}\)
1D
3
NA
20 tháng 3 2022
\(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{89\cdot90}\\ =\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{89}-\dfrac{1}{90}\\ =\dfrac{1}{2}-\dfrac{1}{90}=\dfrac{22}{45}\)
VD
20 tháng 3 2022
\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{89.90}\\ =\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{89}-\dfrac{1}{90}\\ =\dfrac{1}{2}-\left(\dfrac{1}{3}-\dfrac{1}{3}\right)-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)-...-\left(\dfrac{1}{89}-\dfrac{1}{89}\right)-\dfrac{1}{90}\\ =\dfrac{1}{2}-0-0-...-0-\dfrac{1}{90}\\ =\dfrac{1}{2}-\dfrac{1}{90}\\ =\dfrac{45}{90}-\dfrac{1}{90}\\ =\dfrac{44}{90}\\ =\dfrac{22}{45}\)
7 tháng 4 2019
=2(1/2.3+1/3.4+...+1/199.200)
=2(1/2-1/3+1/3-1/4+...+1/99-1/100)
=2(1/2-1/100)
=2 . 49/100
=49/50
TC
2
6 tháng 3 2022
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}=1-\dfrac{1}{100}=\dfrac{99}{100}\)
VH
1
T
2 tháng 9 2023
\(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\cdot\cdot\cdot+\dfrac{1}{18\cdot19}+\dfrac{1}{19\cdot20}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\cdot\cdot\cdot+\dfrac{1}{18}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{20}\)
\(=\dfrac{1}{2}-\dfrac{1}{20}\)
\(=\dfrac{9}{20}\)
#\(Urushi\)☕
NA
2
7 tháng 4 2016
A=1/2.3+1/3.4+1/4.5+..+1/2014.2015
A=1/2-1/3+1/3-1/4+1/4-1/5+...+1/2014-1/2015
A=1/2-1/2015
A=2013/4030
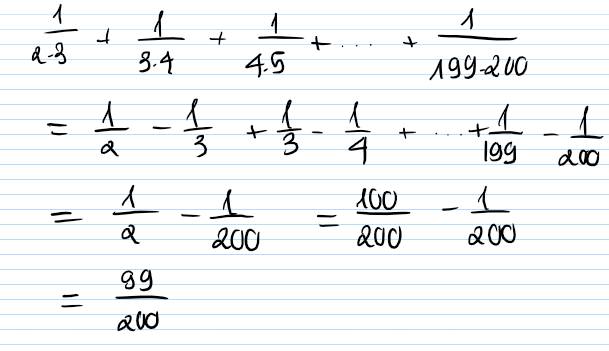
Ta có:
\(\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{199\cdot200}\)
\(=\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{5}\right)+...+\left(\frac{1}{199}-\frac{1}{200}\right)\)
\(=\frac{1}{2}+\left(\frac{1}{3}-\frac{1}{3}\right)+\left(\frac{1}{4}-\frac{1}{4}\right)+...+\left(\frac{1}{199}-\frac{1}{199}\right)+\frac{1}{200}\)
\(=\frac{1}{2}+0+0+...+0+\frac{1}{200}\)
\(=\frac{1}{2}+\frac{1}{200}\)
\(=\frac{1\cdot100}{2\cdot100}+\frac{1}{200}\)
\(=\frac{100}{200}+\frac{1}{200}\)
\(=\frac{101}{200}\)