X2 + 16X+ 64
16X2 - 8X +4
25X2+ 10X +1
X2 - 12X + 36
4X2- 4X + 1
X2 - 2X+ 1
X2 + X+ 1/4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 10 2018
Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:
Pt tương đương:
1 ( x + 1 ) ( x + 3 ) + 1 ( x + 3 ) ( x + 5 ) + 1 ( x + 5 ) ( x + 7 ) + 1 ( x + 7 ) ( x + 9 ) = 1 5
⇔ 2 ( x + 1 ) ( x + 3 ) + 2 ( x + 3 ) ( x + 5 ) + 2 ( x + 5 ) ( x + 7 ) + 2 ( x + 7 ) ( x + 9 ) = 2 5
ĐKXĐ: x ≠ -1; -3; -5; -7; -9
Khi đó:
<=> 1 x + 1 - 1 x + 3 + 1 x + 3 - 1 x + 5 + 1 x + 5 - 1 x + 7 + 1 x + 7 - 1 x + 9 = 2 5
<=> 1 x + 1 - 1 x + 9 = 2 5
<=> 1 ( x + 9 ) - 1 ( x + 1 ) ( x + 1 ) ( x + 9 ) = 2 ( x + 1 ) ( x + 9 ) 5 ( x + 1 ) ( x + 9 )
=> 5[x + 9 – (x + 1)] = 2(x + 1) (x + 9)
ó 5(x + 9 – x – 1) = 2 x 2 + 20x + 18
ó 2 x 2 + 20x – 22 = 0
CM
4 tháng 7 2019
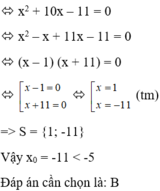
a) Ta có P = 4 x 2 ( x − 2 y ) 2 ( x + 2 y ) 2 . ( x + 2 y ) 2 16 x = x 4 ( x − 2 y ) 2
Với x ≠ 0 , x ≠ ± 2 y
b) Ta có Q = 16 x ( x 2 − 16 ) 2 . x 2 − 16 2 x = 8 16 − x 2 với x ≠ 0 , x ≠ ± 4
2 tháng 8 2017
a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
TN
1 tháng 8 2017
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
= 0 - 0
= 0
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2)
= (x-xx+1) : (2x-2) : (x-xx+1) : (2x-2)
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
= -2x-1-xx2+1. (14 - 4x)
= -x2-1-xx2+14-4x
= -6x-xx2+13
BH
0
CM
8 tháng 1 2017
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
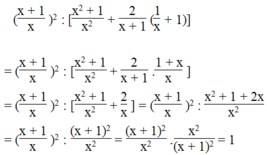
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
Áp dụng hằng đẳng thức
a) x2+16x+64
=> x2+2.8x+82
=> (x+8)2
b) 25x2+10x+1
=> (5x+1)2
c) x2-12x+36
=> (x+6)2
d) 4x2-4x+1
=> (2x-1)2
e) x2-2x+1
=> (x-1)2
Thiếu câu f)
x2+x+1/4
=> (x+1/2)2