Tìm nghiệm nguyên
x3 -3y3 -9z3 =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
3
15 tháng 4 2023
\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+3y^3=2023\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+3y^3=2023\)
\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)+3y^3=2023\) (*)
Đặt \(x^2+8x+11=t\left(t\inℤ;t\ge-5\right)\), pt (*) trở thành \(\left(t-4\right)\left(t+4\right)+3y^3=2023\)
\(\Leftrightarrow t^2-16+3y^3=2023\)
\(\Leftrightarrow t^2+3y^3=2039\) (1)
Xét pt (1), dễ thấy \(t^2\equiv0\left(mod3\right)\) hoặc \(t^2\equiv1\left(mod3\right)\), lại có \(3y^3\equiv0\left(mod3\right)\) nên \(VT\equiv0\left(mod3\right)\) hoặc \(VT\equiv1\left(mod3\right)\). Nhưng \(VP=2039\equiv2\left(mod3\right)\), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên.
16 tháng 4 2023
(x+1)(x+3)(x+5)(x+7)+3y3=2023
⇔[(�+1)(�+7)][(�+3)(�+5)]+3�3=2023⇔[(x+1)(x+7)][(x+3)(x+5)]+3y3=2023
⇔(�2+8�+7)(�2+8�+15)+3�3=2023⇔(x2+8x+7)(x2+8x+15)+3y3=2023 (*)
Đặt �2+8�+11=�(�∈Z;�≥−5)x2+8x+11=t(t∈Z;t≥−5), pt (*) trở thành (�−4)(�+4)+3�3=2023(t−4)(t+4)+3y3=2023
⇔�2−16+3�3=2023⇔t2−16+3y3=2023
⇔�2+3�3=2039⇔t2+3y3=2039 (1)
Xét pt (1), dễ thấy �2≡0(���3)t2≡0(mod3) hoặc �2≡1(���3)t2≡1(mod3), lại có 3�3≡0(���3)3y3≡0(mod3) nên ��≡0(���3)VT≡0(mod3) hoặc ��≡1(���3)VT≡1(mod3). Nhưng ��=2039≡2(���3)VP=2039≡2(mod3), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên
PT
1
AH
Akai Haruma
Giáo viên
18 tháng 3 2021
Lời giải:
PT $\Leftrightarrow x^3+3x-5=x^2y+2y=y(x^2+2)$
$\Rightarrow y=\frac{x^3+3x-5}{x^2+2}$
Để $y$ nguyên thì $x^3+3x-5\vdots x^2+2$
$\Leftrightarrow x(x^2+2)+x-5\vdots x^2+2$
$\Leftrightarrow x-5\vdots x^2+2(1)$
$\Rightarrow x^2-5x\vdots x^2+2$
$\Leftrightarrow x^2+2-(5x+2)\vdots x^2+2$
$\Leftrightarrow 5x+2\vdots x^2+2(2)$
Từ $(1);(2)\Rightarrow 5(x-5)-(5x+2)\vdots x^2+2$
$\Leftrightarrow 27\vdots x^2+2$. Do $x^2+2\geq 2$ nên:
$\Rightarrow x^2+2\in\left\{3;9;27\right\}$
$\Rightarrow x^2\in\left\{1;7;25\right\}$
Do $x$ nguyên nên $x\in\left\{\pm 1; \pm 5\right\}$
Thay vào $y$ ta tìm được:
$x=-1\Rightarrow y=-3$
$x=5\Rightarrow y=5$
9 tháng 1 2021
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
9 tháng 1 2021
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
CM
10 tháng 6 2019
Điều kiện: x > - 5
Xét dấu hàm số f x = x x - 3 x + 3
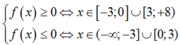
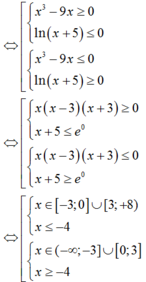
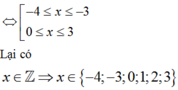
Chọn C.
TC
6 tháng 5 2022
a) cho A(x) = 0
\(=>2x^2-4x=0\)
\(x\left(2-4x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)\(B\left(y\right)=4y-8\)
cho B(y) = 0
\(4y-8=0\Rightarrow4y=8\Rightarrow y=2\)
c)\(C\left(t\right)=3t^2-6\)
cho C(t) = 0
\(=>3t^2-6=0=>3t^2=6=>t^2=2\left[{}\begin{matrix}t=\sqrt{2}\\t=-\sqrt{2}\end{matrix}\right.\)
TC
6 tháng 5 2022
d)\(M\left(x\right)=2x^2+1\)
cho M(x) = 0
\(2x^2+1=0\Rightarrow2x^2=-1\Rightarrow x^2=-\dfrac{1}{2}\left(vl\right)\)
vậy M(x) vô nghiệm
e) cho N(x) = 0
\(2x^2-8=0\)
\(2\left(x^2-4\right)=0\)
\(2\left(x^2+2x-2x-4\right)=0\)
\(2\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
7 tháng 3 2022
Ta có: \(x^3-2y^2=2^3-2\cdot\left(-2\right)^2=8-8=0\)
Do đó: C=0
NB
7 tháng 3 2022
thay x=2; y=-2 vào \(x^3-2y^2=2^3-2\left(-2\right)^2=8-8=0\)
\(\Rightarrow C=0\)
ko hiểu thì nhìn ở trên các số nhân với nhau nhưng mà lại có 1 thừa số =0 nên cả cái biểu thức =0
Chú ý: Bài này trình bày rất ngắn gọn, bạn nên thêm vài yếu tố thiết yếu để làm phong phú bài toán hơn. Chúc thành công ':(
Tìm nghiệm nguyên của phương trình:
\(x^3-3y^3-9z^3=0\) \(\left(1\right)\)
\(--------\)
Từ \(\left(1\right)\) suy ra \(x^3=9z^3+3y^3\) \(\left(2\right)\)
Rõ ràng ta nhận thấy, vế trái của pt \(\left(2\right)\) chia hết cho \(3\) nên \(x^3\) phải chia hết cho \(3\)
Tức là \(x\) phải chia hết cho \(3\)
Khi đó, đặt \(x=3x_1\) (với \(x_1\in Z\) )
Thay vào \(\left(2\right)\) , ta có:
\(\left(2\right)\) \(\Leftrightarrow\) \(27x^3_1=9z^3+3y^3\) \(\Leftrightarrow\) \(y^3=9x^3_1-3z^3\) \(\left(3\right)\)
Lý luận như trên, ta có \(y\) chia hết cho \(3.\) Đặt \(y=3y_1\) (với \(y_1\in Z\) )
Biến đổi tương tự, ta được:
\(z^3=3x^3_1-9y^3_1\) \(\left(4\right)\)
Lý luận như trên, ta có \(z\) chia hết cho \(3.\) Đặt \(z=3z_1\) (với \(z_1\in Z\) )
Biến đổi tương tự, ta lại có:
\(\left(4\right)\) \(\Leftrightarrow\) \(27z^3_1=3x^3_1-9y^3_1\) \(\Leftrightarrow\) \(x^3_1-3y^3_1-9z^3_1=0\) \(\left(5\right)\)
Rõ ràng nếu bộ số gồm các ẩn \(\left(x_0;y_0;z_0\right)\) là nghiệm của pt \(\left(1\right)\) thì bộ số \(\left(\frac{x_0}{3};\frac{y_0}{3};\frac{z_0}{3}\right)\) cũng là nghiệm của \(\left(1\right),\) hơn nữa \(\left(x_0;y_0;z_0\right)\) là các số lẻ và \(\left(\frac{x_0}{3};\frac{y_0}{3};\frac{z_0}{3}\right)\) cũng là số lẻ. Quá trình trên cứ tiếp tục được lặp mãi và các số \(\left(\frac{x_0}{3^n};\frac{y_0}{3^n};\frac{z_0}{3^n}\right)\) là các số lẻ với mọi số \(n\) nguyên dương
Vậy, \(x=y=z=0\)
Bài ngắn tới nỗi mà mù mắt luôn