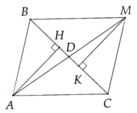
Cho tam giác ABC cạnh AB=4,AC=6,BC=8 gọi M là trung điểm của BC và D là trung điểm của BM .Tính DA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
24 tháng 3 2017
nếu không áp dụng công thức tính đường trung tuyến thì có cách khác không ạ ?
YN
11 tháng 7 2023
\(a,\)
Xét \(\triangle ADC\) và \(\triangle MDB\):
\(DA=DM\)
\(DC=DB\)
\(\widehat{ADC}=\widehat{MDB}\)
\(\Rightarrow\Delta ADC=\Delta MDB\left(c.g.c\right)\) \(\left(1\right)\)
\(\left(1\right)\Rightarrow AC=BM\)
\(\Rightarrow\widehat{ACD}=\widehat{MBD}\)
mà hai góc này nằm ở vị trí so le trong
\(\Rightarrow\)\(AC//BM\)
\(b,\)
\(\left(1\right)\Rightarrow\widehat{DAC}=\widehat{DMB}\)
Xét \(\triangle ABM\) và \(\triangle MCA\):
\(AM\) chung
\(BM=AC\)
\(\widehat{DAC}=\widehat{DMB}\)
\(\Rightarrow\Delta ABM=\Delta MCA\left(c.g.c\right)\).
11 tháng 7 2023
a: Xét tứ giác ABMC có
D là trung điểm chung của AM và BC
=>ABMC là hình bình hành
=>AC//BM và AC=BM
b: Xét ΔABM và ΔMCA có
AB=MC
BM=CA
AM chung
=>ΔABM=ΔMCA
7 tháng 3 2017
Vì M là trung điểm của BC nên:BM=MC=8:2=4 (cm)
mà BD=1:2BM Vậy BD=2(CM)
Vậy AD=8(CM)
6 tháng 12 2021
1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
6 tháng 12 2021
1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
6 tháng 12 2021
1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
18 tháng 12 2021
a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD