Giúp tôi vớii
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\widehat{xOm};\widehat{nOm}\)
\(\widehat{nOm};\widehat{yOn}\)
\(\widehat{yOn};\widehat{xOn}\)
\(\widehat{xOm};\widehat{yOm}\)
b: \(\widehat{yOn};\widehat{xOn}\)
\(\widehat{xOm};\widehat{yOm}\)
c: \(\widehat{mOy}=180^0-30^0=150^0\)
\(\widehat{nOx}=180^0-50^0=130^0\)
\(\widehat{mOn}=180^0-80^0=100^0\)

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;-7\right)\\\overrightarrow{BC}=\left(4;8\right)\\\overrightarrow{AC}=\left(8;1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BC}+\overrightarrow{AC}=\left(12,9\right)\)
\(\Rightarrow\overrightarrow{AB}.\left(\overrightarrow{BC}+\overrightarrow{AC}\right)=4.12-7.9=...\)
b. Gọi \(H\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x+3;y-5\right)\\\overrightarrow{BH}=\left(x-1;y+2\right)\\\end{matrix}\right.\)
Do \(AH\perp BC\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow4\left(x+3\right)+8\left(y-5\right)=0\)
\(\Rightarrow x+2y=7\) (1)
Do H thuộc BC \(\Rightarrow\dfrac{x-1}{4}=\dfrac{y+2}{8}\Rightarrow2x-y=4\Rightarrow y=2x-4\)
Thế vào (1) \(\Rightarrow x+2\left(2x-4\right)=7\Rightarrow x=3\Rightarrow y=2\)
\(\Rightarrow H\left(3;2\right)\)



Nếu A1 = 10%; A2=20%
Tỉ lệ %A của gen là:%A=\(\dfrac{\%A_1+\%A_2}{2}\)=%T→%G=%X=50%−%A=35%
a. trên mạch 1 :
A1=T2=10%;G1=X2=30%;A2=T1=20%;X1=G2=2×%G−%G1=40%
Vậy : A=T=15% ; G=X=35%
A1=10%;T1=20%;G1=30%;T1=40%
A2=20%;T2=10%;G2=40%;T2=30%


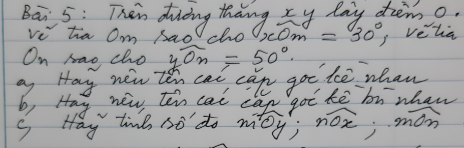 giúp em vớii
giúp em vớii





 giúp mình vớii
giúp mình vớii
`Answer:`
a. \(\frac{5}{16}-\frac{5}{24}\)
\(=\frac{15}{48}-\frac{10}{48}\)
\(=\frac{5}{48}\)
b. \(-\frac{5}{8}+\frac{12}{7}+\frac{13}{8}+\frac{2}{7}\)
\(=\left(-\frac{5}{8}+\frac{13}{8}\right)+\left(\frac{12}{7}+\frac{2}{7}\right)\)
\(=1+2\)
\(=3\)
c. \(\frac{2}{1.2}+\frac{2}{2.3}+\frac{2}{3.4}+...+\frac{2}{99.100}\)
\(=2.\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\right)\)
\(=2.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\right)\)
\(=2.\left(1-\frac{1}{100}\right)\)
\(=2.\frac{99}{100}\)
\(=\frac{99}{50}\)