cho x + y = 5, x.y = 4 tính:
A = x2 + y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MP
24 tháng 7 2023
\(a.2x\left(x-1\right)-3\left(x^2+4x\right)+x\left(x+2\right)\)
\(=2x^2-2x-3x^2-12x+x^2+2x\)
\(=-12x\)
\(b.\left(2x-3\right)\left(3x+5\right)-\left(x-1\right)\left(6x+2\right)+3-5x\)
\(=6x+10x-9x^2-15-6x^2-2x-6x-2+3-5x\)
\(=-15x^2+3x-14\)
\(c.\left(x-y\right)\left(x^2+xy+y^2\right)-\left(x+y\right)\left(x^2-y^2\right)\)
\(=x^3-y^3-x^3+y^3+x^2y-y^3\)
\(=y^3+x^2y\)
NM
4
2 tháng 9 2021
a) \(3\left(2x-3\right)+5\left(x+2\right)=6x-9+5x+10=11x+1\)
b) \(3x\left(2x-8\right)+\left(6x+2\right)\left(5-x\right)=6x^2-24x+30x-6x^2+10-2x=4x+10\)
c) \(\left(x-3\right)\left(x+3\right)-\left(x-5\right)^2=x^2-9-x^2+10x-25=10x-34\)
d) \(\left(x-y\right)^3-\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-3x^2y+3xy^2-y^3-x^3+y^3=3xy^2-3x^2y\)
13 tháng 12 2021
\(a,=4x^2+12xy+9y^2\\ b,=25x^2-10xy+y^2\\ d,=4x^2+4xy^2+y^4\\ e,=9x^4-12x^2y+4y^2\\ g,=x^3+64\)
AH
Akai Haruma
Giáo viên
9 tháng 9 2021
Lời giải:
a.
$(2x-3)^2+(2x+3)(5-2x)=(4x^2-12x+9)-(-4x^2+4x+15)$
$=4x^2-12x+9+4x^2-4x-15$
$=24-8x$
b.
$3(2x-3)+5(x+2)=6x-9+5x+10=11x+1$
c.
$3x(2x-8)+(6x-2)(5-x)=(6x^2-24x)+(-6x^2+32x-10)$
$=6x^2-24x-6x^2-32x+10$
$=8x-10$
d.
$(x-3)(x+3)-(x-5)^2=(x^2-9)-(x^2-10x+25)$
$=x^2-9-x^2+10x-25=10x-34$
e.
$(x-y)^3-(x-y)(x^2+xy+y^2)=(x^3-3x^2y+3xy^2-y^3)-(x^3-y^3)$
$=-3x^2y+3xy^2=3xy(y-x)$
9 tháng 9 2021
a: ta có: \(\left(2x-3\right)^2+\left(2x+3\right)\left(5-2x\right)\)
\(=4x^2-12x+9+2x-4x^2+15-6x\)
\(=-16x+24\)
b: Ta có: \(3\left(2x-3\right)+5\left(x+2\right)\)
\(=6x-9+5x+10\)
\(=11x+1\)
c: ta có: \(3x\left(2x-8\right)+\left(6x-2\right)\left(5-x\right)\)
\(=6x^2-24x+30x-6x^2-10+2x\)
\(=8x-10\)
DT
1
11 tháng 12 2023
a: \(\dfrac{\left(x^2+2x-y^2+1\right)}{x-y+1}\)
\(=\dfrac{\left(x^2+2x+1\right)-y^2}{x+1-y}\)
\(=\dfrac{\left(x+1\right)^2-y^2}{\left(x+1-y\right)}=\dfrac{\left(x+1+y\right)\left(x+1-y\right)}{\left(x+1-y\right)}=x+1+y\)
20 tháng 10 2021
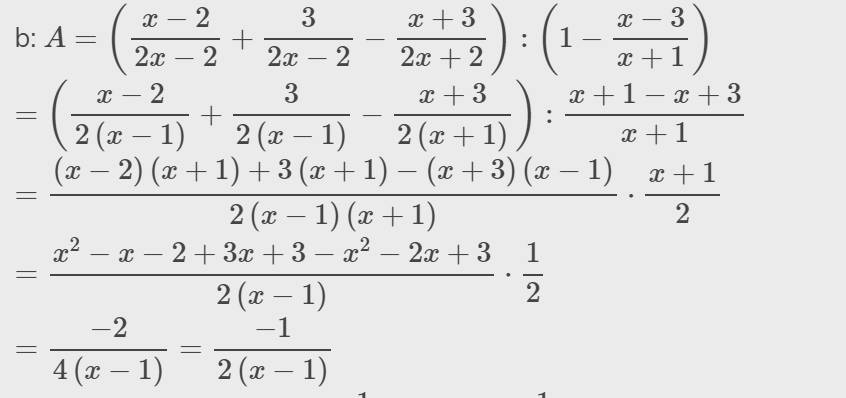
\(x-y=-30\Rightarrow\dfrac{x}{-30}=\dfrac{1}{y}\\ y.z=-42\\ \Rightarrow\dfrac{z}{-42}=\dfrac{1}{y}\\ \Rightarrow\dfrac{x}{-30}=\dfrac{z}{-42}\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{-30}=\dfrac{z}{-42}=\dfrac{z-x}{-42-\left(-30\right)}=\dfrac{-12}{-12}=1\)
\(\dfrac{x}{-30}=1\Rightarrow x=-30\\ \dfrac{z}{-42}=1\Rightarrow z=-42\)
\(x.y=-30\Rightarrow-30.y=-30\Rightarrow y=1\)
5 tháng 10 2021
a: \(\left(\dfrac{1}{3}x+2y\right)\left(\dfrac{1}{9}x^2-\dfrac{2}{3}xy+4y^2\right)=\dfrac{1}{27}x^3+8y^3\)
b: \(\left(x^2-\dfrac{1}{3}\right)\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)=x^6-\dfrac{1}{27}\)
c: \(\left(y-5\right)\left(y^2+5y+25\right)=y^3-125\)
CM
21 tháng 1 2018
Ta có
(I): 4 x 2 + 4 x – 9 y 2 + 1 = ( 4 x 2 + 4 x + 1 ) – 9 y 2 = ( 2 x + 1 ) 2 – ( 3 y ) 2
= (2x + 1 + 3y)(2x + 1 – 3y) nên (I) đúng
Và
(II):
5 x 2 – 10 x y + 5 y 2 – 20 z 2 = 5 ( x 2 – 2 x y + y 2 – 4 z 2 ) = 5 [ ( x – y ) 2 – ( 2 z ) 2 ]
= 5(x – y – 2z)(x – y + 2z) nên (II) sai
Đáp án cần chọn là: A
x^2 +y^2=(x+y)^2-2xy=25-8=17
k nhé
\(x^2+2xy+y^2=\left(x+y\right)^2\)
\(x^2+y^2=\left(x+y\right)^2-2xy\)
\(A=x^2+y^2\)
\(=\left(x+y\right)^2-2xy\)
Thay x + y = 5 và xy = 4 vào A, ta có:
\(5^2-2\times4=25-8=17\)
Vậy A = 17 tại khi x + y = 5 và xy = 4