Tìm giá trị nhỏ nhất của biểu thức: P=x2 + y2 - xy - x + y + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 3 2018
Ta có: 2 x 2 + 1 2 ≥ 2 x ; 2 y 2 + 1 2 ≥ 2 y và x 2 + y 2 ≥ 2 x y
Cộng vế với vế các BĐT trên ta được:
3 x 2 + y 2 + 1 ≥ 2 x + y + x y = 5 2
=> A = x 2 + y 2 ≥ 1 2
Từ đó tìm được A m i n = 1 2 <=> x = y = 1 2
DH
18 tháng 4 2021
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
24 tháng 5 2021
\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 5 2021
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
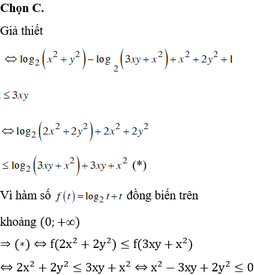
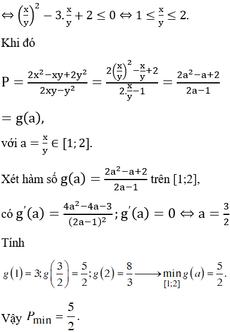
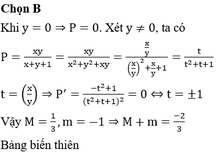
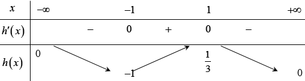
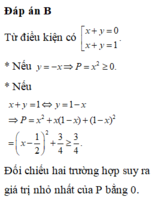
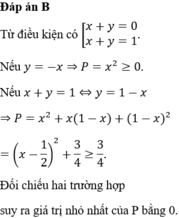
Có P = x^2 +y^2-xy-x+y+1
=> 2A =2x^2 + 2y^2 -2xy -2x +2y+2 =(x^2 -2xy +y^2)+ (x^2 -2x+1) +(y^2 +2y +1) =(x-y)^2 +(x-1)^2 +(y+1)^2 >=0
=> Min A =0
Còn lại bạn tự giải nka!@
mk mới học lớp 6 nên chưa biết được nhiều nhak xin lỗi
Ta có: \(P=x^2+y^2-xy-x+y+1\)
\(\Rightarrow4P=4x^2+4y-4xy-4x+4y+4\)
\(=\left(4x^2-4xy+y^2\right)-2\left(2x-y\right)+3y^2+2y+4\)
\(=\left(2x-y\right)^2-2\left(2x-y\right)+1+3\left(y^2+\frac{2}{3}y+\frac{1}{9}\right)+\frac{8}{3}\)
\(=\left[\left(2x-y\right)-1\right]^2+3\left(y+\frac{1}{3}\right)^2+\frac{8}{3}\)
\(=\left(2x-y-1\right)^2+3\left(y+\frac{1}{3}\right)^2+\frac{8}{3}\)
Vậy min4P = \(\frac{8}{3}\Rightarrow minP=\frac{2}{3}\)
\(P_{min}=\frac{2}{3}\Leftrightarrow\hept{\begin{cases}y+\frac{1}{3}=0\\2x-y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=\frac{-1}{3}\\x=\frac{1}{3}\end{cases}}\)