g iup tui voi moi nguoi
iup tui voi moi nguoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



THAM KHẢO CÁCH RÚT GỌN DÒNG 3: Chứng minh đẳng thức lượng giác sin^4a + cos^4a = 1 - 1/2 sin^2 2a = 3/4 + 1/4 cos4a câu hỏi 1063664 - hoidap247.com
\(M=\sin^4\alpha\left(1+2\cos^2\alpha\right)+\cos^4\alpha\left(1+2\sin^2\alpha\right)\\ M=\left(\sin^4\alpha+\cos^4\alpha\right)+2\sin^2\alpha\cdot\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)\\ M=\dfrac{3}{4}+\dfrac{1}{4}\cos4\alpha+\dfrac{1}{2}\sin^22\alpha\cdot1\\ M=\dfrac{3}{4}+\dfrac{1}{4}\cos4\alpha+\dfrac{1}{2}\sin^22\alpha\)

1. used to
2. is used to
3. used to
4. used to
5. was used to
6. am used to
7. used to
8. am used to
9. used to
10. used to
11. work
12. working
13. living
14. get
1.used to 2.is used to 3.used to 4.used to 5.is used to 6.am used to 7.used to 8.am used to 9.used to 10.used to 11.work 12.working 13.living 14.get up

TH1: 1,2 đứng đầu
=>Có \(2\cdot2\cdot4=16\left(cách\right)\)
TH2: 1,2 đứng giữa
Nếu số 0 đứng cuối thì có \(2\cdot1\cdot4=8\left(cách\right)\)
Nếu số 8 đứng cuối thì có \(2\cdot1\cdot3=6\left(cách\right)\)
=>Có 14 cách
TH3: 1,2 đứng cuối
=>Có \(1\cdot4\cdot3=12\left(cách\right)\)
=>Có 16+14+12=42 cách

1 cooks
2 didn't go - was
3 are you doing - am washing
4 isn't writing - think - is playing
5 Did she eat
6 usually drink - am having
7 saw - was
8 is singing - likes - took - felt
9 did he draw
10 always has - doesn't like

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{12}=\dfrac{b}{9}=\dfrac{c}{8}=\dfrac{a+b+c}{12+9+8}=\dfrac{87}{29}=3\)
Do đó: a=36; b=27; c=24


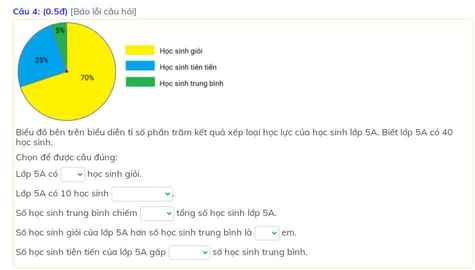
Lớp 5A có 28 học sinh giỏi.
Lớp 5A có 10 học sinh tiên tiến.
Số học sinh trung bình chiếm 5% tổng số học sinh lớp 5A.
Số học sing giỏi cửa lớp 5A hơn số học sinh trung bình là 26 em.
Số học sinh tiên tiến của lớp 5A gấp 5 lần số học sinh trung bình.

d: Ta có: \(\sqrt{x\sqrt{x}-7}=1\)
\(\Leftrightarrow x\sqrt{x}-7=1\)
\(\Leftrightarrow\left(\sqrt{x}\right)^3=8\)
\(\Leftrightarrow x=4\)
\(a,ĐK:x\ge\dfrac{1}{3}\\ PT\Leftrightarrow\left|x-3\right|=3x-1\\ \Leftrightarrow\left[{}\begin{matrix}x-3=3x-1\left(x\ge3\right)\\x-3=1-3x\left(x< 3\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\Leftrightarrow x=1\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|1-2x\right|=5\\ \Leftrightarrow\left[{}\begin{matrix}1-2x=5\left(x\le\dfrac{1}{2}\right)\\2x-1=5\left(x>\dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:x\ge0\\ PT\Leftrightarrow\left|6x-2\right|=x\\ \Leftrightarrow\left[{}\begin{matrix}6x-2=x\left(x\ge\dfrac{1}{3}\right)\\6x-2=-x\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{5}\left(tm\right)\\x=\dfrac{2}{7}\left(tm\right)\end{matrix}\right.\\ d,ĐK:x\ge\sqrt[3]{49}\\ PT\Leftrightarrow x\sqrt{x}-7=1\\ \Leftrightarrow\sqrt{x^3}=8\\ \Leftrightarrow x^3=64\Leftrightarrow x=4\left(tm\right)\)
\(e,ĐK:x\le2\\ PT\Leftrightarrow4\left(x^2+7\right)=\left(2-x\right)^2\\ \Leftrightarrow4x^2+28=4-4x+x^2\\ \Leftrightarrow3x^2+4x+24=0\\ \Delta'=2^2-24\cdot3=-68< 0\\ \Leftrightarrow x\in\varnothing\)