giup e vs ạ huhu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 8 2021
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(60^0< 120^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
Suy ra: \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
hay \(\widehat{yOz}=60^0\)
b) Ta có: tia Oy nằm giữa hai tia Ox và Oz(cmt)
mà \(\widehat{xOy}=\widehat{yOz}\left(=60^0\right)\)
nên Oy là tia phân giác của \(\widehat{xOz}\)
DT
12 tháng 2 2022
c/tiếp tục áp dụng công thức bậc 2 :
(a=12;b=-25;c=12) có:
\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2.a}\)
\(\Leftrightarrow x=\dfrac{-1.-25\pm\sqrt{-25^2-4.12.12}}{2.12}\)
\(\Leftrightarrow x=\dfrac{25\pm\sqrt{49}}{24}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{25+7}{24}\\x_2=\dfrac{25-7}{24}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{4}{3}\\x_2=\dfrac{3}{4}\end{matrix}\right.\)
từ trên suy ra:
\(\dfrac{3}{4}\le x\le\dfrac{4}{3}\)
DT
12 tháng 2 2022
b/áp dụng công thức bậc 2 :
\(x=\dfrac{-1.-3\pm\sqrt{3^2-4.2.-2}}{2.2}\)
\(\Leftrightarrow x=\dfrac{3\pm\sqrt{25}}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{3-5}{4}\\x_2=\dfrac{3+5}{4}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=2\end{matrix}\right.\)
Trên pc cj vẽ khó qué e tự nghiên cứu hỏi lại thầy cô nhe:<
\(\Rightarrow x\le-\dfrac{1}{2};x\ge2\)
\(\Rightarrow x\in\left\{-\infty;-\dfrac{1}{2}\right\}U\left\{\infty;2\right\}\)
25 tháng 5 2022
b: Vì (d)//y=-2x+5/2 nên a=-2
Vậy: y=-2x+b
Phương trình hoành độ giao điểm là:
\(0.5x^2+2x-b=0\)
\(\Delta=2^2-4\cdot0.5\cdot\left(-b\right)=4+2b\)
Để (d) tiếp xúc với (P) thì 2b+4=0
hay b=-2
MH
25 tháng 5 2022
Gọi số kg vật liệu xưởng phải sản xuất mỗi ngày theo kế hoạch là \(x\left(kg\right)\left(0< x< 216\right)\)
Thời gian dự định sản xuất là \(\dfrac{216}{x}\) (ngày)
Ba ngày đầu tiên khối lượng vật liệu sản xuất được là \(3x\left(kg\right)\)
Số vật liệu còn lại là \(232-3x\)
Thời gian sản xuất số vật liệu còn lại là \(\dfrac{232-3x}{x+8}\)
Ta có phương trình:
\(\dfrac{216}{x}=3+\dfrac{232-3x}{x+8}+1\)
\(\Rightarrow216\left(x+8\right)=4x\left(x+8\right)+\left(232-3x\right)x\)
\(\Rightarrow216x+1728=4x^2+32x+232x-3x^2\)
\(\Rightarrow x^2+48x-1728=0\Rightarrow\left[{}\begin{matrix}x=24\left(TM\right)\\x=-72\left(L\right)\end{matrix}\right.\)
Vậy theo kế hoạch mỗi ngày xưởng phải sản xuất 24 kg vật liệu.
VD
25 tháng 5 2022
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
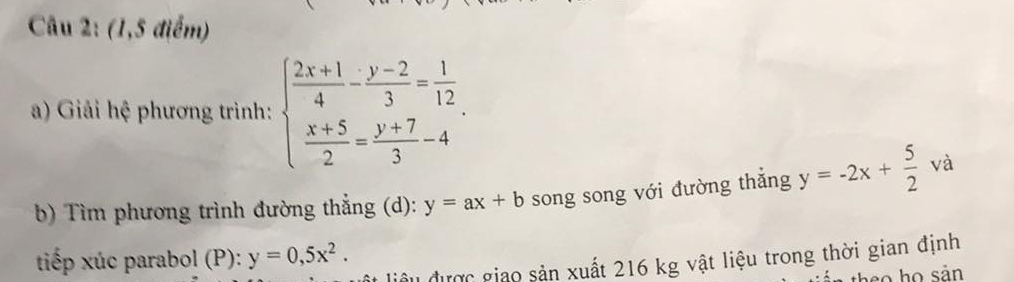
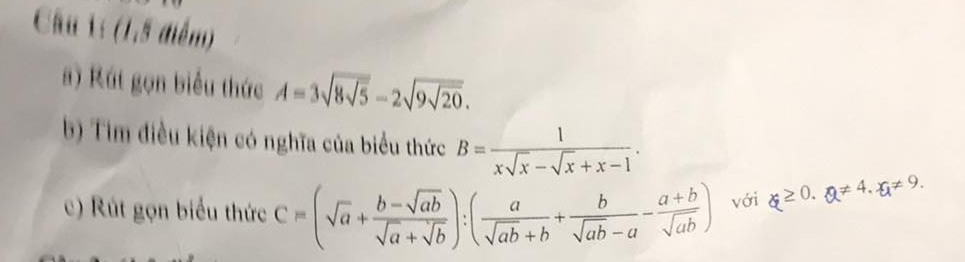
a: Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{15}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{2}\)
mà AD+CD=AC=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{2}=\dfrac{AD+CD}{3+2}=\dfrac{15}{5}=3\)
=>\(AD=3\cdot3=9cm;CD=2\cdot3=6\left(cm\right)\)
b: Xét ΔABC có BD' là phân giác góc ngoài
nên \(\dfrac{D'C}{D'A}=\dfrac{BC}{BA}\)
=>\(\dfrac{D'C}{D'C+CA}=\dfrac{10}{15}=\dfrac{2}{3}\)
=>\(\dfrac{D'C}{D'C+15}=\dfrac{2}{3}\)
=>\(3D'C=2\left(D'C+15\right)\)
=>D'C=30(cm)