Cho đường tròn tâm O và 2 điểm A,B nằm bên ngoài đường tròn dựng đường kính COD sao cho AC=BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Cách dựng
- Dựng A’ đối xứng với A qua tâm O của đường tròn
- Dựng đường thẳng x là trung trực của A’B
- Gọi giao điểm của đường thẳng x và đường tròn (O) là D
- Dựng đường kính COD
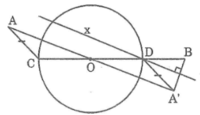
* Chứng minh
Ta có: OA = OA’ và OD = OC
Suy ra tứ giác ACA’D là hình bình hành
Suy ra: AC = A’D
Lại có: A’D = BD (tính chất đường trung trực)
Suy ra: AC = BD



Biện luận :
Tùy theo số giao điểm của d và đường tròn (O) là 2, 1, 0 mà bài toán có 2, 1, 0 nghiệm hình.
(Trên hình 89, bài toán có 2 nghiệm hình)

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA
=>AI*AO=2R^2
Xét ΔBDE vuông tại D có DC vuông góc BE
nên ΔBDE vuông tại D
=>BC*BE=BD^2=4R^2
=>BC*BE+AI*AO=6R^2

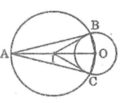
* Phân tích
Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán
Ta có: AB ⊥ OB ⇒ ∠ ABO = 90 °
AC ⊥ OC ⇒ ∠ ACO = 90 °
Tam giác ABO có ∠ ABO = 90 ° nội tiếp trong đường tròn đường kính AO và tam giác ACO có ∠ ACO = 90o nội tiếp trong đường tròn đường kính AO.
Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).
* Cách dựng
- Dựng I là trung điểm của OA
- Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C
- Nối AB, AC ta được hai tiếp tuyến cần dựng
* Chứng minh
Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ABO = 90 °
Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O)
Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ACO = 90 °
Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)
* Biện luận
Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).