tìm GTNN
A = X2 + 10x + 30 + y + 2y
B= Z2 _ 6Z _ 8 + T2 + 4T
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
$A=x^2+y^2-6x+4y+20=(x^2-6x+9)+(y^2+4y+4)+7$
$=(x-3)^2+(y+2)^2+7\geq 0+0+7=7$
Vậy $A_{\min}=7$. Giá trị này đạt tại $(x-3)^2=(y+2)^2=0$
$\Leftrightarrow x=3; y=-2$
---------------------
$B=9x^2+y^2+2z^2-18x+4z-6y+30$
$=(9x^2-18x+9)+(y^2-6y+9)+(2z^2+4z+2)+10$
$=9(x^2-2x+1)+(y^2-6y+9)+2(z^2+2z+1)+10$
$=9(x-1)^2+(y-3)^2+2(z+1)^2+10\geq 10$
Vậy $B_{\min}=10$. Giá trị này đạt tại $(x-1)^2=(y-3)^2=(z+1)^2$
$\Leftrightarrow x=1; y=3; z=-1$
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
$C=x^2+y^2+z^2-xy-yz-xz+3$
$2C=2x^2+2y^2+2z^2-2xy-2yz-2xz+6$
$=(x^2-2xy+y^2)+(y^2-2yz+z^2)+(x^2-2xz+z^2)+6$
$=(x-y)^2+(y-z)^2+(z-x)^2+6\geq 6$
$\Rightarrow C\geq 3$
Vậy $C_{\min}=3$. Giá trị này đạt tại $x-y=y-z=z-x=0$
$\Leftrihgtarrow x=y=z$
--------------------------------------
$D=5x^2+2y^2+4xy-2x+4y+2021$
$=2(y^2+2xy+x^2)+3x^2-2x+4y+2021$
$=2(x+y)^2+4(x+y)+3x^2-6x+2021$
$=2(x+y)^2+4(x+y)+2+3(x^2-2x+1)+2016$
$=2[(x+y)^2+2(x+y)+1]+3(x^2-2x+1)+2016$
$=2(x+y+1)^2+3(x-1)^2+2016\geq 2016$
Vậy $D_{\min}=2016$ khi $x+y+1=x-1=0$
$\Leftrightarrow x=1; y=-2$
TT
1
T
21 tháng 8 2023
\(D=x^4+4xy+4y^2-z^2+2xt-t^2\)
\(=\left[x^2+2.x.2y+\left(2y\right)^2\right]-\left(z^2-2.z.t+t^2\right)\)
\(=\left(x+2y\right)^2-\left(z-t\right)^2\)
\(=\left(x+2y-z+t\right)\left(x+2y+z-t\right)\)
Với \(x=10;y=40;z=30;t=20\):
\(D=\left(10+2.40-30+20\right)\left(10+2.40+30-20\right)\)
\(=\left(10+80-10\right)\left(10+80+10\right)\)
\(=80.100=8000\)
Vậy \(D=8000\)
HA
0
CM
29 tháng 7 2017
Đáp án A
Phương pháp
Giả sử mặt phẳng (b) cắt mặt cầu (S ) theo đường tròn có bán kính r
Mặt cầu (S) có tâm I, bán kính R và d(I; β ) = R ta có R 2 = r 2 + d 2
Cách giải
Mặt phẳng (b) cắt mặt cầu (S) theo đường tròn có bán kính r = 8 π 2 π = 4
Mặt cầu (S) có tâm I(-1;2;3) bán kính R = 17 - m
Ta có
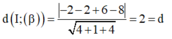
Áp dụng định lí Pytago ta có
NT
0
1 tháng 4 2022
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
x^2+4y^2+z^2-2x-6z+8y+15
=x^2+4y^2+z^2-2x-6z+8y+1+1+4+9
=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1
=(x-1)^2+4(y+1)^2+(z-3^)2+1
Ta thấy:(x−1)^2≥0
4(y+1)^2≥0
(z−3)^ 2≥0
{(x−1)^24(y+1)^2(z−3)^2≥0
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
⇒(x−1)2+4(y+1)2+(z−3)2+1≥0+1=1>0
TU
0
