Tìm x nguyên để A chia hết cho B biết :
A = 10x\(^2\)- 7x -5
B = 2x - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
b) g(x) = x³ - 4x² + 5x - 1 = x³ - 3x² - x² + 3x + 2x - 6 + 5 = x²(x-3) - x(x-3) + 2(x-3) + 5
g(x) chia hết cho x-3 khi và chỉ khi 5 chia hết cho x-3 (5 là số nguyên tố nên chỉ xét các trường hợp)
TH1: x-3 = -5 <=> x = -2
TH2: x-3 = -1 <=> x = 2
TH3: x-3 = 1 <=> x = 4
TH4: x-3 = 5 <=> x = 8
Vậy có giá trị nguyên của x thỏa là {-1, 2, 4, 8}

a: =>2x^3-4x^2-3x^2+6x+4x-8+a+8 chia hết cho x-2
=>a+8=0
=>a=-8
b: =>2x^3+x^2-x^2-0,5x-0,5x+0,25+m-0,25 chia hết cho 2x+1
=>m-0,25=0
=>m=0,25

Để đa thức 10x^2 - 7x + a chia hết cho 2x - 3, ta cần xác định giá trị của a.
Theo lý thuyết chia đa thức, nếu đa thức chia hết cho 2x - 3 thì trải nghiệm của 2x - 3 sẽ là giá trị của x khi đa thức bằng 0.
Vì vậy, để tìm giá trị của a, ta có thể đặt 10x^2 - 7x + a = 0 và giải phương trình này khi x = 3/2 (do 2x - 3 = 0).
Thay x = 3/2 vào phương thức:
10(3/2)^2 - 7(3/2) + a = 0
Đơn giản hóa:
10(9/4) - 21/2 + a = 0
90/4 - 42/4 + a = 0
48/4 + a = 0
12 + a = 0
một = -12
Vì vậy, giá trị của a là -12 để đa thức 10x^2 - 7x + a chia hết cho 2x - 3.

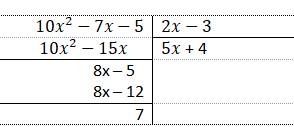
Để \(A⋮B\) thì \(7⋮\left(2x-3\right)\)
\(\Rightarrow2x-3\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow2x\in\left\{-4;2;4;10\right\}\)
\(\Rightarrow x\in\left\{-2;1;2;5\right\}\)

Câu 1:
\(\Leftrightarrow10x^2-15x+8x-12+a+12⋮2x-3\)
=>a+12=0
hay a=-12
Câu 2;
Để A là số nguyên thì \(\left(x+2\right)⋮x^2+4\)
\(\Leftrightarrow x^2-4⋮x^2+4\)
\(\Leftrightarrow x^2+4-8⋮x^2+4\)
\(\Leftrightarrow x^2+4\in\left\{4;8\right\}\)
hay \(x\in\left\{0;2;-2\right\}\)

a) \(x^3-5x^2+8x-4=\left(x^3-x^2\right)-4\left(x^2-x\right)+4\left(x-1\right)=x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2-4x+4\right)=\left(x-1\right)\left(x-2\right)^2\)
b) \(A=5x\left(2x-3\right)+4\left(2x-3\right)+7\) chia hết cho 2x-3 => 7 chia hết cho 2x -3
=> 2x -3 thuộc U(7) ={-7;-1;1;7}
+2x-3 =-7 => x =-2
+2x-3 =-1 => x =1
+2x-3 =1 => x =2
+2x -3 =7 => x =5
Ta xét : \(\frac{A}{B}=\frac{10x^2-7x-5}{2x-3}=\frac{\left(5x+4\right)\left(2x-3\right)+7}{2x-3}=5x+4+\frac{7}{2x-3}\)
Để A chia hết cho B thì 7 chia hết cho (2x-3)
Suy ra 2x-3 thuộc ước của 7 (chú ý điều kiện x khác 3/2)
Liệt kê ra là xong bạn nhé ^^