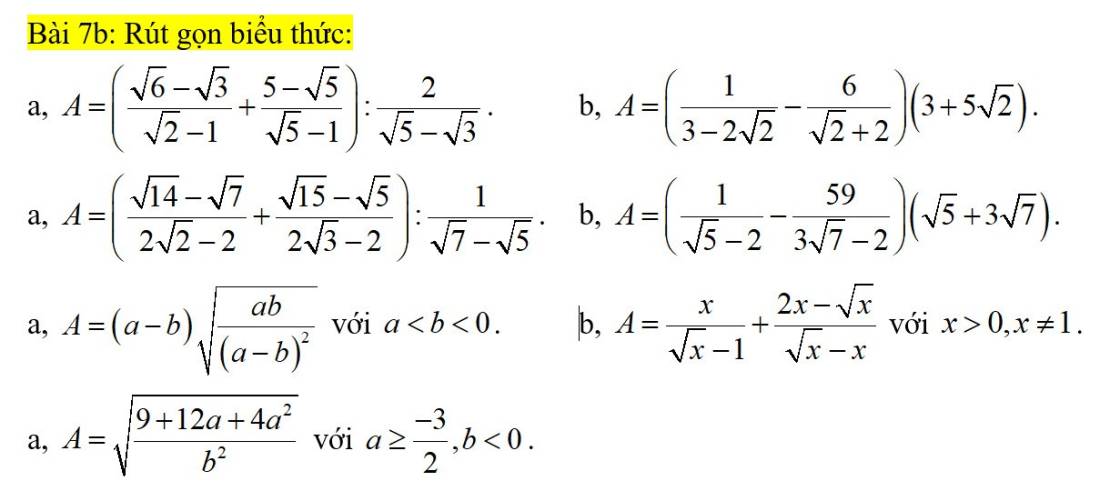làm câu 5 nhé
làm câu 5 nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


that is a 10-year-old girl.
he is a careful driver
how much is a hat?
my house is not far from my school.
Phuong is the tallest in my class
i have a dozen of eggs.
that is a 10-year-old girl.
he is a careful driver
how much is a hat?
my house is not far from my school.
Phuong is the tallest in my class
i have a dozen of eggs.

a) \(\left|x-3\right|\ge0\)
\(\Rightarrow\left|x-3\right|+2021\ge2021\)
\(\Rightarrow A\ge\dfrac{2020}{2021}\)
Dấu = xảy ra khi x = 3
Vậy:............
b) Ta có: \(\left\{{}\begin{matrix}\left(x-\dfrac{3}{5}\right)^2\ge0\\\left|y+1\right|\ge0\end{matrix}\right.\)
PT => \(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-1\end{matrix}\right.\)



\(P=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{x-9}\)
\(=\dfrac{x-\sqrt{x}-6}{x-9}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{x-9}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)
4:
a: P>4/5
=>P-4/5>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{4}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-4\sqrt{x}-12}{5\sqrt{x}+15}>0\)
=>\(\sqrt{x}-2>0\)
=>x>4
b: \(P>\dfrac{2\sqrt{x}}{5}\)
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{2\sqrt{x}}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-2x-6\sqrt{x}}{5\sqrt{x}+15}>0\)
=>\(-2x-\sqrt{x}+10>0\)
=>\(-2x-5\sqrt{x}+4\sqrt{x}+10>0\)
=>\(\left(2\sqrt{x}+5\right)\left(-\sqrt{x}+2\right)>0\)
=>\(-\sqrt{x}+2>0\)
=>0<=x<4
5:
a: \(P-\dfrac{1}{2}=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{1}{2}\)
\(=\dfrac{2\sqrt{x}+4-\sqrt{x}-3}{2\sqrt{x}+6}=\dfrac{\sqrt{x}+1}{2\sqrt{x}+6}>0\)
=>P>1/2
b: \(P-1=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-1=\dfrac{\sqrt{x}+2-\sqrt{x}-3}{\sqrt{x}+3}\)
\(=\dfrac{-1}{\sqrt{x}+3}< 0\)
\(P^2-P=P\left(P-1\right)\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\cdot\dfrac{-1}{\sqrt{x}+3}< 0\)
=>P^2<P
=>P>P^2

a: \(A=\left(\dfrac{\sqrt{6}-\sqrt{3}}{\sqrt{2}-1}+\dfrac{5-\sqrt{5}}{\sqrt{5}-1}\right):\dfrac{2}{\sqrt{5}-\sqrt{3}}\)
\(=\left(\dfrac{\sqrt{3}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right):\dfrac{2\left(\sqrt{5}+\sqrt{3}\right)}{2}\)
\(=\dfrac{\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{3}+\sqrt{5}}=1\)
a:
\(A=\left(\dfrac{\sqrt{14}-\sqrt{7}}{2\sqrt{2}-2}+\dfrac{\sqrt{15}-\sqrt{5}}{2\sqrt{3}-2}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}+\sqrt{5}}{2}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}=\dfrac{7-5}{2}=1\)
a:
\(A=\left(a-b\right)\cdot\sqrt{\dfrac{ab}{\left(a-b\right)^2}}\)
\(=\left(a-b\right)\cdot\dfrac{\sqrt{ab}}{\left|a-b\right|}\)
a<b<0
=>a-b<0
=>\(A=\left(a-b\right)\cdot\dfrac{\sqrt{ab}}{-\left(a-b\right)}=-\sqrt{ab}\)
a:
\(A=\sqrt{\dfrac{9+12a+4a^2}{b^2}}\)
\(=\sqrt{\dfrac{\left(2a+3\right)^2}{b^2}}=\left|\dfrac{2a+3}{b}\right|\)
a>=-3/2
=>2a+3>=0
b<0
=>\(\dfrac{2a+3}{b}< =0\)
=>\(A=\dfrac{-\left(2a+3\right)}{b}\)
b:
\(A=\left(\dfrac{1}{3-2\sqrt{2}}-\dfrac{6}{2+\sqrt{2}}\right)\left(3+5\sqrt{2}\right)\)
\(=\left(\dfrac{3+2\sqrt{2}}{1}-\dfrac{6\left(2-\sqrt{2}\right)}{2}\right)\left(3+5\sqrt{2}\right)\)
\(=\left(3+2\sqrt{2}-3\left(2-\sqrt{2}\right)\right)\cdot\left(3+5\sqrt{2}\right)\)
\(=\left(5\sqrt{2}-3\right)\left(5\sqrt{2}+3\right)\)
=50-9
=41
b:
\(A=\left(\dfrac{1}{\sqrt{5}-2}-\dfrac{59}{3\sqrt{7}-2}\right)\left(3\sqrt{7}+\sqrt{5}\right)\)
\(=\left(\dfrac{\sqrt{5}+2}{5-4}-\dfrac{59\left(3\sqrt{7}+2\right)}{63-4}\right)\left(3\sqrt{7}+\sqrt{5}\right)\)
\(=\left(\sqrt{5}+2-3\sqrt{7}-2\right)\left(3\sqrt{7}+\sqrt{5}\right)\)
\(=\left(\sqrt{5}-3\sqrt{7}\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
=5-63
=-58
b:
\(A=\dfrac{x}{\sqrt{x}-1}+\dfrac{2x-\sqrt{x}}{\sqrt{x}-x}\)
\(=\dfrac{x}{\sqrt{x}-1}-\dfrac{2x-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-1}=\sqrt{x}-1\)
 Làm hộ mình câu 5 thôi nhé !
Làm hộ mình câu 5 thôi nhé !



 làm câu 5 thôi nhé
làm câu 5 thôi nhé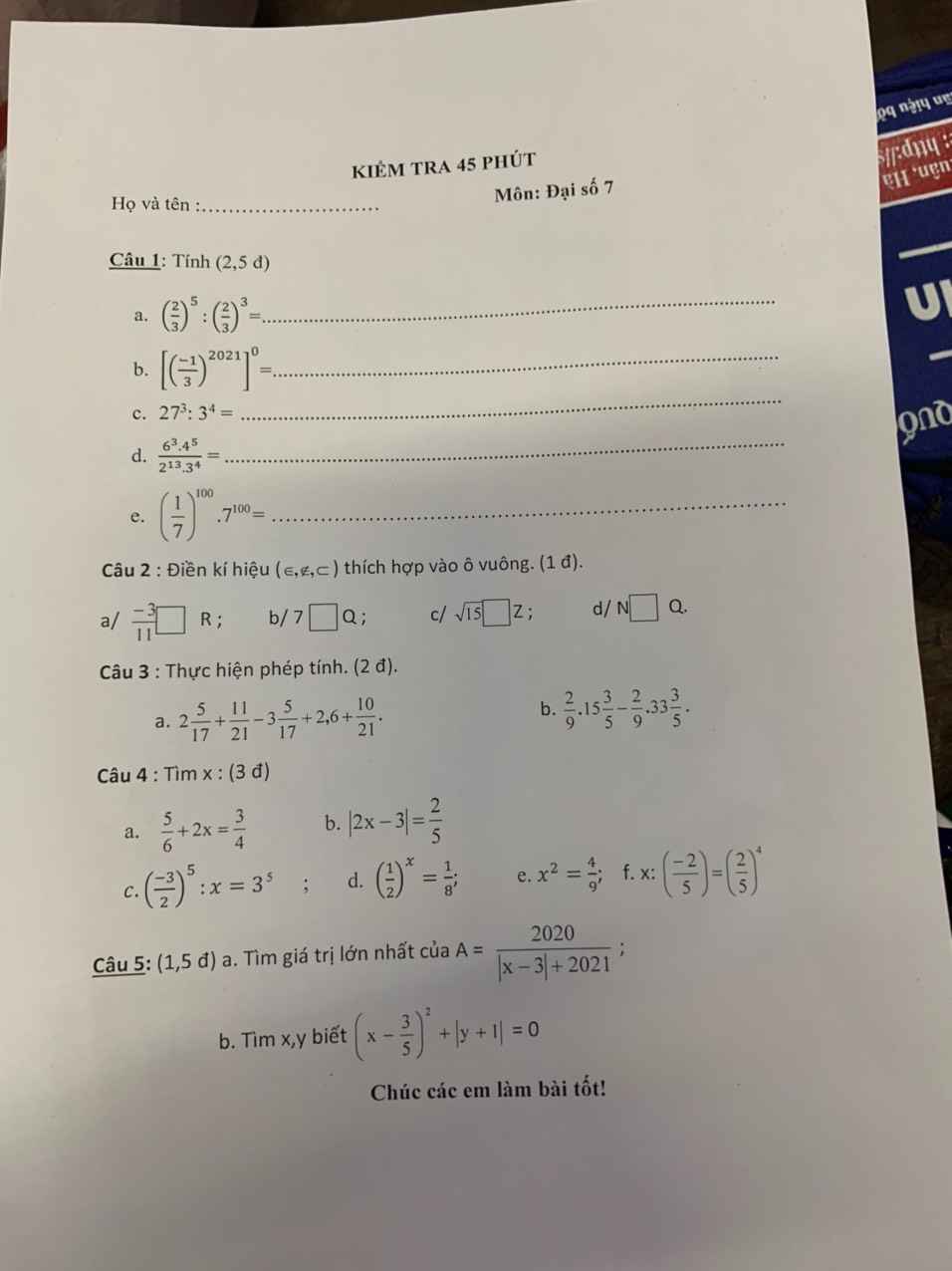


 các bạn giúp mk làm câu 5 nhé
các bạn giúp mk làm câu 5 nhé