\(lim\dfrac{4n^5+n^3-5n+3}{\left(2n^2-3\right)\left(2n+1\right)^3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a=\lim\left(\dfrac{2n^3\left(5n+1\right)+\left(2n^2+3\right)\left(1-5n^2\right)}{\left(2n^2+3\right)\left(5n+1\right)}\right)\)
\(=\lim\left(\dfrac{2n^3-13n^2+3}{\left(2n^2+3\right)\left(5n+1\right)}\right)=\lim\dfrac{2-\dfrac{13}{n}+\dfrac{3}{n^3}}{\left(2+\dfrac{3}{n^2}\right)\left(5+\dfrac{1}{n}\right)}=\dfrac{2}{2.5}=\dfrac{1}{5}\)
\(b=\lim\left(\dfrac{n-2}{\sqrt{n^2+n}+\sqrt{n^2+2}}\right)=\lim\dfrac{1-\dfrac{2}{n}}{\sqrt{1+\dfrac{1}{n}}+\sqrt{1+\dfrac{2}{n}}}=\dfrac{1}{2}\)
\(c=\lim\dfrac{\sqrt{1+\dfrac{3}{n^3}-\dfrac{2}{n^4}}}{2-\dfrac{2}{n}+\dfrac{3}{n^2}}=\dfrac{1}{2}\)
\(d=\lim\dfrac{\sqrt{1-\dfrac{4}{n}}-\sqrt{4+\dfrac{1}{n^2}}}{\sqrt{3+\dfrac{1}{n^2}}-1}=\dfrac{1-2}{\sqrt{3}-1}=-\dfrac{1+\sqrt{3}}{2}\)

\(lim\left(5n-\sqrt{25n^2-3n+5}\right)=lim\dfrac{25n^2-25n^2+3n-5}{5n+\sqrt{25n^2-3n+5}}\)
\(=lim\dfrac{3n-5}{5n+\sqrt{25n^2-3n+5}}=lim\dfrac{3-\dfrac{5}{n}}{5+\sqrt{25-\dfrac{3}{n}+\dfrac{5}{n^2}}}=\dfrac{3-0}{5+\sqrt{25-0+0}}=\dfrac{3}{10}\)
\(lim\dfrac{4n^5-3n^4-2n^3+7n-9}{-5n\left(3n^2-3n+1\right)\left(5-2n^2\right)}=lim\dfrac{\dfrac{4n^5-3n^4-2n^3+7n-9}{n^5}}{\dfrac{-5n}{n}\dfrac{\left(3n^2-3n+1\right)}{n^2}\dfrac{\left(5-2n^2\right)}{n^2}}\)
\(=lim\dfrac{4-\dfrac{3}{n}-\dfrac{2}{n^2}+\dfrac{7}{n^4}-\dfrac{9}{n^5}}{-5.\left(3-\dfrac{2}{n}+\dfrac{1}{n^2}\right).\left(\dfrac{5}{n^2}-2\right)}=\dfrac{4-0-0+0-0}{-5\left(3-0+0\right).\left(0-2\right)}=\dfrac{2}{15}\)

1) \(\lim\limits_{n\rightarrow\infty}\dfrac{6n-8}{n-1}=\lim\limits_{n\rightarrow\infty}\dfrac{2n\left(1-\dfrac{4}{n}\right)}{n\left(1-\dfrac{1}{n}\right)}=2\)
2) \(\lim\limits_{n\rightarrow\infty}\dfrac{n^2+5n-3}{4n^3-2n+5}=\lim\limits_{n\rightarrow\infty}\dfrac{n^2\left(1+\dfrac{5}{n}-\dfrac{3}{n^2}\right)}{n^3\left(4-\dfrac{2}{n^2}+\dfrac{5}{n^3}\right)}=\dfrac{1}{4n}=\infty\)
3) \(\lim\limits_{n\rightarrow\infty}\left(-2n^5+4n^4-3n^2+4\right)=\lim\limits_{n\rightarrow\infty}n^5\left(-2+\dfrac{4}{n}-\dfrac{3}{n^2}+\dfrac{4}{n^5}\right)=-2n^5=-\infty\)

a/ Bạn coi lại đề bài, 3n^2 +n^2 thì bằng 4n^2 luôn chứ ko ai cho đề bài như vậy cả
b/ \(\lim\limits\dfrac{\dfrac{n^3}{n^3}+\dfrac{3n}{n^3}+\dfrac{1}{n^3}}{-\dfrac{n^3}{n^3}+\dfrac{2n}{n^3}}=-1\)
c/ \(=\lim\limits\dfrac{-\dfrac{2n^3}{n^2}+\dfrac{3n}{n^2}+\dfrac{1}{n^2}}{-\dfrac{n^2}{n^2}+\dfrac{n}{n^2}}=\lim\limits\dfrac{-2n}{-1}=+\infty\)
d/ \(=\lim\limits\left[n\left(1+1\right)\right]=+\infty\)
e/ \(\lim\limits\left[2^n\left(\dfrac{2n}{2^n}-3+\dfrac{1}{2^n}\right)\right]=\lim\limits\left(-3.2^n\right)=-\infty\)
f/ \(=\lim\limits\dfrac{4n^2-n-4n^2}{\sqrt{4n^2-n}+2n}=\lim\limits\dfrac{-\dfrac{n}{n}}{\sqrt{\dfrac{4n^2}{n^2}-\dfrac{n}{n^2}}+\dfrac{2n}{n}}=-\dfrac{1}{2+2}=-\dfrac{1}{4}\)
g/ \(=\lim\limits\dfrac{n^2+3n-1-n^2}{\sqrt{n^2+3n-1}+n}+\lim\limits\dfrac{n^3-n^3+n}{\sqrt[3]{\left(n^3-n\right)^2}+n.\sqrt[3]{n^3-n}+n^2}\)
\(=\lim\limits\dfrac{\dfrac{3n}{n}-\dfrac{1}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{3n}{n^2}-\dfrac{1}{n^2}}+\dfrac{n}{n}}+\lim\limits\dfrac{\dfrac{n}{n^2}}{\dfrac{\sqrt[3]{\left(n^3-n\right)^2}}{n^2}+\dfrac{n\sqrt[3]{n^3-n}}{n^2}+\dfrac{n^2}{n^2}}\)
\(=\dfrac{3}{2}+0=\dfrac{3}{2}\)

\(\lim\dfrac{\left(2n-1\right)\left(3n^2+2\right)^3}{-2n^5+4n^3-1}=\lim\dfrac{\left(\dfrac{2n-1}{n}\right)\left(\dfrac{3n^2+2}{n^2}\right)^3}{\dfrac{-2n^5+4n^3-1}{n^7}}\)
\(=\lim\dfrac{\left(2-\dfrac{1}{n}\right)\left(3+\dfrac{2}{n^2}\right)^3}{-\dfrac{2}{n^2}+\dfrac{4}{n^4}-\dfrac{1}{n^7}}=-\infty\)
\(\lim3^n\left(6.\left(\dfrac{2}{3}\right)^n-5+\dfrac{7n}{3^n}\right)=+\infty.\left(-5\right)=-\infty\)

\(lim\dfrac{\left(2-n\right)\left(3+2n^3\right)}{2n^2-1}=lim\dfrac{\left(\dfrac{2}{n}-1\right)\left(\dfrac{3}{n}+2n^2\right)}{2-\dfrac{1}{n^2}}=-\infty\)
\(\dfrac{lim\left(\sqrt{4n^2+1}-2n\right)n}{\sqrt[3]{4-n^3}+n}=lim\dfrac{n\left(\sqrt[3]{\left(4-n^3\right)^2}-n\sqrt[3]{4-n^3}+n^2\right)}{4.\left(\sqrt{4n^2+1}+2n\right)}\)
\(=lim\dfrac{\sqrt[3]{\left(n^3-4\right)^2}+n\sqrt[3]{n^3-4}+n^2}{4\left(\sqrt{4+\dfrac{1}{n^2}}+2\right)}=+\infty\)

Dang này thì cứ chọn số hạng có mũ cao nhất trên tử và mẫu là được. Nó là ngắt vô cùng lớn hay bé gì đấy
\(=lim\dfrac{8n^6}{3n^6}=\dfrac{8}{3}\)
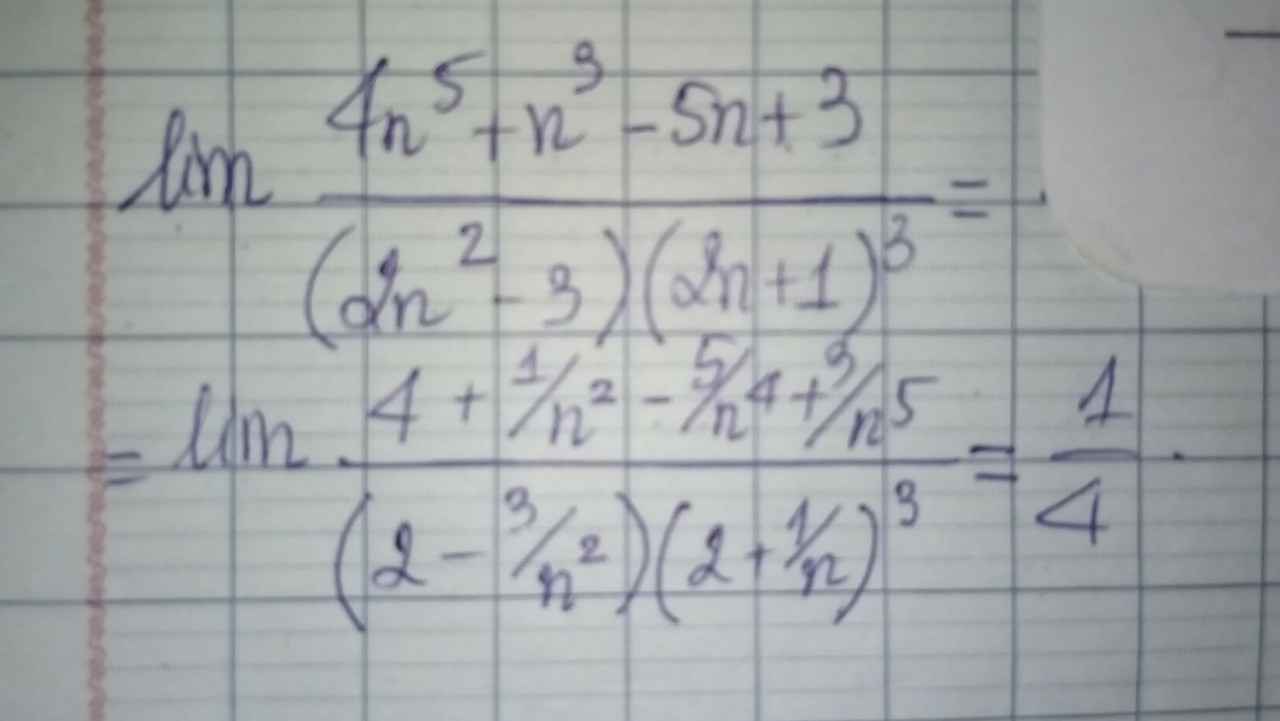
Lời giải:
\(\lim \frac{4n^5+n^3-5n+3}{(2n^2-3)(2n+1)^3}=\lim \frac{4+\frac{1}{n^2}-\frac{5}{n^4}+\frac{3}{n^5}}{(2-\frac{3}{n^2})(2+\frac{1}{n})^3}=\frac{4}{2.2^3}=\frac{1}{4}\)