Giúp e tìm công thức tổng quát với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)

41.
Số hạng tổng quát của khai triển \(\left(x^2+x\right)^{10}\):
\(T_{k+1}=C^k_{10}.\left(x^2\right)^{10-k}.x^k=C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}\)


1. Phát biểu, viết biểu thức tổng quát, lấy ví dụ minh họa tính chất giao hoán của phép cộng số tự nhiên?
- Lí thuyết: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi
- Công thức: a + b = b + a
- VD: 2 + 3 = 3 + 2
2. Phát biểu, viết biểu thức tổng quát, lấy ví dụ minh họa tính chất kết hợp của phép cộng số tự nhiên?
- Lý thuyết: Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
- Công thức: (a + b) + c = a + (b + c)
- VD: (4 + 5) + 3 = 4 + (3 + 5)
3. Phát biểu, viết biểu thức tổng quát, lấy ví dụ minh họa tính chất cộng với số 0 của phép cộng số tự nhiên?
- Lý thuyết: Bất kì số tự nhiên nào cộng với 0 cũng bằng chính số đó
- Công thức: a + 0 = 0 + a = a
- VD: 8 + 0 = 0 + 8 = 8
Bài tập.
Vận dụng các tính chất của phép cộng thực hiện các phép tính
a) 12 + 88 + 56
= (12 + 88) + 56
= 100 + 56
= 156
b) 12 + 56 + 88
= (12 + 88) + 56
= 100 + 56
= 156
c) 204 – 204 + 2021
= (204 - 204) + 2021
= 0 + 2021
= 2021
d) 132 + 237 + 868 + 763
= (132 + 868) + (237 + 763)
= 1000 + 1000
= 2000
e) 29 + 132 + 237 + 868 + 763
= 29 + (132 + 868) + (237 + 763)
= 29 + 1000 + 1000
= 29 + 2000
= 2029
g) 652 + 327 + 148 + 15 + 73
= (652 + 148) + (327 + 73) + 15
= 800 + 400 + 15
= 1200 + 15
= 1215
a 156 b 156 c 2021 d 2000 e 2029 g 1215 sorry anh ko có nhiều thời gian nên chỉ viết dc kết quả thôi


Ta có : 2n - 5 ⋮ n + 1
<=> 2n + 2 - 7 ⋮ n + 1
<=> 2(n + 1) - 7 ⋮ n + 1
Vì 2(n + 1) ⋮ n + 1 √ n ∈ Z , Để 2(n + 1) - 7 ⋮ n + 1 <=> 7 ⋮ n + 1
=> n + 1 ∈ Ư(7) = { ± 1; ± 7 }
Ta có : n + 1 = - 7 => n = - 7 - 1 = - 8 (loại)
n + 1 = - 1 => n = - 1 - 1 = - 2 (loại)
n + 1 = 1 => n = 1 - 1 = 0 (TM)
n + 1 = 7 => n = 7 - 1 = 6 (TM)
Vậy với n ∈ { 0; 6 } thì 2n - 5 ⋮ n + 1

\(u_{n+1}=\sqrt{1+u_n^2}\left(1\right)\)
\(u_1=3=\sqrt{9}\)
\(u_2=\sqrt{1+u_1^2}=\sqrt{10}\)
\(u_3=\sqrt{1+u_2^2}=\sqrt{11}\)
...
Dự đoán công thức:\(u_n=\sqrt{n+8}\),\(n\ge1\) (*)
Thật vậy
+)\(n=1,(*)\)\(\Leftrightarrow u_1=3\) (lđ)
+)Giả sử (*) đúng với mọi \(n=k,k>1\)
\((*)\Leftrightarrow u_k=\sqrt{k+8}\)
+)\(n=k+1,\) thay vào (1) có: \(u_{k+2}=\sqrt{1+u^2_{k+1}}=\sqrt{1+\left(\sqrt{1+u_k^2}\right)^2}=\sqrt{2+u^2_k}=\sqrt{2+k+8}=\sqrt{10+k}\)
\(\Rightarrow\)(*) đúng với n=k+1
Vậy CTSHTQ: \(u_n=\sqrt{n+8}\), \(n\ge1\)
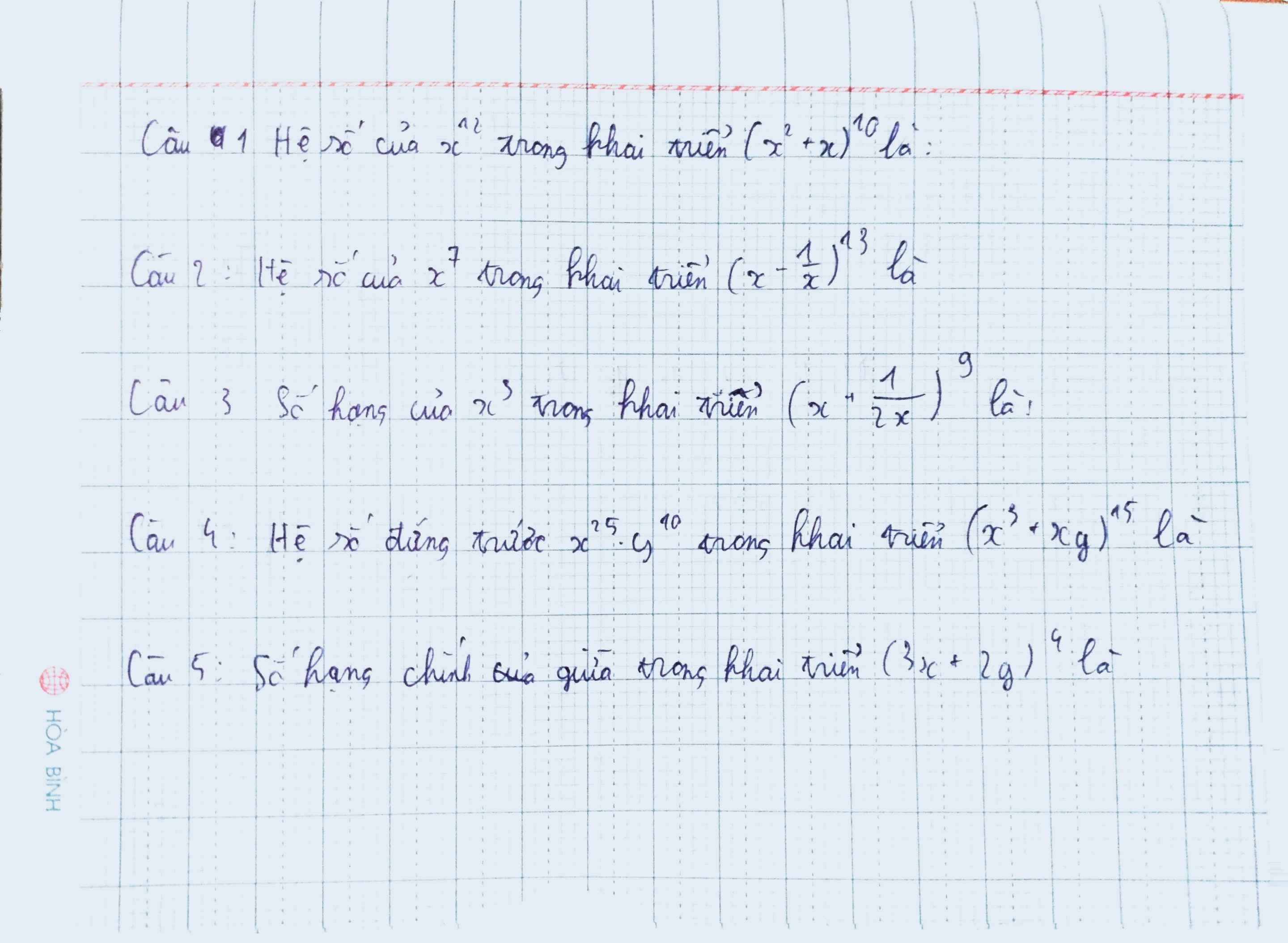

9.
Đặt \(u_n=2v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{2015}{2}\\2v_{n+1}=8v_n^3-6v_n\end{matrix}\right.\) \(\Rightarrow v_{n+1}=4v_n^3-3v_n\)
Xét số thực a là nghiệm lớn hơn của pt:
\(a^2-2v_1a+1=0\Rightarrow\left\{{}\begin{matrix}a=v_1+\sqrt{v_1^2-1}\\\dfrac{1}{a}=v_1-\sqrt{v_1^2-1}\end{matrix}\right.\)
Khi đó ta có:
\(v_1=\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\)
\(v_2=4v_1^3-3v_1=4\left[\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\right]^3-3\left[\dfrac{1}{2}\left(a+\dfrac{1}{a}\right)\right]\)
\(=\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)=\dfrac{1}{2}\left(a^{3^1}+\dfrac{1}{a^{3^1}}\right)\)
\(v_3=4v_2^3-3v_2=4\left[\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)\right]^3-3\left[\dfrac{1}{2}\left(a^3+\dfrac{1}{a^3}\right)\right]=\dfrac{1}{2}\left(a^9+\dfrac{1}{a^9}\right)=\dfrac{1}{2}\left(a^{3^2}+\dfrac{1}{a^{3^2}}\right)\)
Từ đó, ta tổng quát được: \(v_n=\dfrac{1}{2}\left(a^{3^{n-1}}+\dfrac{1}{a^{3^{n-1}}}\right)\)
Ta chứng minh bằng quy nạp:
- Với \(n=1;2;3\) đúng như đã kiểm chứng ở trên
- Giả sử đúng với \(n=k\) hay \(v_k=\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\)
Ta cần chứng minh: \(v_{k+1}=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)\)
Ta có: \(v_{k+1}=4\left[\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\right]^3-3\left[\dfrac{1}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)\right]\)
\(=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)+\dfrac{3}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)-\dfrac{3}{2}\left(a^{3^{k-1}}+\dfrac{1}{a^{3^{k-1}}}\right)=\dfrac{1}{2}\left(a^{3^k}+\dfrac{1}{a^{3^k}}\right)\) (đpcm)
Vậy SHTQ của dãy là: \(u_n=2v_n=a^{3^{n-1}}+\dfrac{1}{a^{3^{n-1}}}\) với \(a\) là nghiệm lớn của pt: \(x^2-2015x+1=0\)
10.
Ta có: \(u_1=1=tan\dfrac{\pi}{4}=tan\dfrac{\pi}{2^2}\)
\(u_2=\dfrac{\sqrt{1+tan^2\dfrac{\pi}{4}}-1}{tan\dfrac{\pi}{4}}=\sqrt{2}-1=tan\dfrac{\pi}{8}=tan\dfrac{\pi}{2^3}\)
Dự đoán: \(u_n=tan\dfrac{\pi}{2^{n+1}}\)
Ta chứng minh bằng quy nạp
Với \(n=1;2\) đúng (đã kiểm chứng ở trên)
Giả sử điều đó đúng với \(n=k\) hay \(u_k=tan\dfrac{\pi}{2^{k+1}}\)
Ta cần chứng minh: \(u_{k+1}=tan\dfrac{\pi}{2^{k+2}}\)
Thật vậy, ta có:
\(u_{k+1}=\dfrac{\sqrt{1+u_k^2}-1}{u_k}=\dfrac{\sqrt{1+tan^2\dfrac{\pi}{2^{k+1}}}-1}{tan\dfrac{\pi}{2^{k+1}}}=\dfrac{\dfrac{1}{cos\dfrac{\pi}{2^{k+1}}}-1}{tan\dfrac{\pi}{2^{k+1}}}\)
\(=\dfrac{1-cos\dfrac{\pi}{2^{k+1}}}{sin\dfrac{\pi}{2^{k+1}}}=\dfrac{2sin^2\dfrac{\pi}{2^{k+2}}}{2sin\dfrac{\pi}{2^{k+2}}.cos\dfrac{\pi}{2^{k+2}}}=tan\dfrac{\pi}{2^{k+2}}\) (đpcm)