mọi người giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.







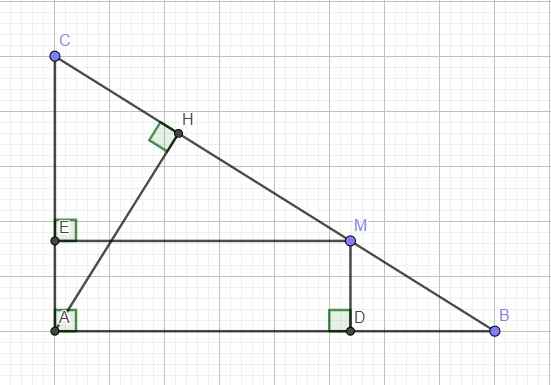
Theo giả thiết: \(ME\perp AC\Rightarrow\Delta MEA\) vuông tại E \(\Rightarrow\) E thuộc đường tròn đường kính AM (1)
Tương tự, tam giác MDA vuông tại D \(\Rightarrow\) D thuộc đường tròn đường kính AM (2)
Tam giác MHA vuông tại H \(\Rightarrow\) H thuộc đường tròn đường kính AM (3)
(1);(2);(3) \(\Rightarrow\) 5 điểm A, D, M, H, E cùng thuộc đường tròn đường kính AM (đpcm)

Lời giải:
Mình sẽ xác định giúp bạn tập hợp. Việc biểu diễn nó trên trục số thì có lẽ đơn giản rồi.
1. $(2;9)\cap (1;4)=(2;4)$
2. $(-\infty; -2)\cup (-3;5)=(-\infty; 5)$
3. $[3;1]\cap (-2;0)=$ \(\varnothing\)
4.\((-2;1)\setminus [0;3)=(-2;0)\)
5. \((-\infty; -2]\setminus (-3;5)=(-\infty; -3]\)
6. $[3;+\infty)\cap (-2;-0)=\varnothing$
7. $[1;2]\setminus [0;3)=[1;0)$
8.$[-4;3)\cup [3;5]=[-4;5]$
9. $(-\infty;3)\setminus (-4;-1)=\varnothing$







 mọi người giúp em với ạ 🥺
mọi người giúp em với ạ 🥺
\(=\lim n^2\left(-4+\dfrac{1}{\sqrt{n}}-\dfrac{2}{n^2}\right)\)
Do \(\lim n^2=+\infty\)
\(\lim\left(-4+\dfrac{1}{\sqrt[]{n}}-\dfrac{2}{n^2}\right)=-4+0-0=-4< 0\)
\(\Rightarrow\lim n^2\left(-4+\dfrac{1}{\sqrt[]{n}}-\dfrac{2}{n^2}\right)=-\infty\)