Sự khác biệt giữa đường chéo của hòh thoi và hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 5 2018
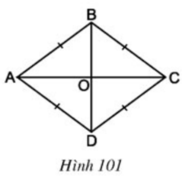
a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất cắt nhau tại trung điểm mỗi đường
b) Xét ΔAOB và ΔCOB
AB = CB
BO chung
OA = OC ( O là trung điểm AC )
⇒ ΔAOB = ΔCOB (c.c.c)
⇒ (AOB) = (COB) ,(ABO) = (CBO) (các cặp góc tương ứng)
(ABO) = (CBO) ⇒ BO là phân giác góc ABC
(AOB) + (COB) = 180o ⇒(AOB) = (COB) = 180o : 2 = 90o
Chứng minh tương tự, ta kết luận được:
AC, BD là các đường phân giác của các góc của hình thang
và AC ⊥ BD tại O
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Các định lí trên có thể được phát biểu là:
a) Một phương trình bậc hai có biệt thức dương là điều kiện cần và đủ để có hai nghiệm phân biệt
b) Một hình bình hành có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để nó là hình thoi.
8 tháng 4 2022
a: \(S=37\cdot20=740\left(cm^2\right)\)
b: Độ dài đường chéo thứ hai là:
270x2:18=30(cm)
VQ
8 tháng 4 2022
đổi : 2 dm = 20 cm
diện tích hình bình hành là:
37 x 20 : 2 = 370 ( cm)
17 tháng 7 2015
diện tích hình thoi là:
18 x 14 : 2 = 126 (dm2)
độ dài đáy hình bình hành là:
126 : 9 = 14 (dm)
17 tháng 7 2015
Diện Tích hình thoi là:
18x14:2= 126 (dm2)
Độ dài cạnh đáy của hình bình hành là:
126:9= 14 (dm)
Đáp số: 14dm
8 tháng 8 2015
A B C D M N
Có thể nói rõ hơn ở đề bài là M thuộc canh AB mà AM x 3 = AB. Nếu chỉ cho AM x 3 = AB thì có rất nhiều điểm M thỏa mãn
+) Nối M với C chia hình bình hành thành 2 phần có diện tích bằng nhau
S(AMC) = S(AMNC) /2 = 20 cm2
+) Tam giác CAB và CAM có chung chiều cao hạ từ C xuống AB; đáy AM = 1/3 đáy AB
=> S(CAB) = 3 x S(AMC) = 30 cm2
+) S(ABCD) = 60 x 2 = 120 cm2
=> BD = S(ABCD) x 2 : AC = 120 x 2 : 24 = 10 cm
Các đường chéo của một hình thoi chia đôi góc vuông tạo thành hai hình tam giác. Trái ngược với hình bình hành có các đường chéo chia đôi nhau tạo thành hai hình tam giác đồng dạng.
khác mỗi cái tên thằng súc vật, thằng óc chó