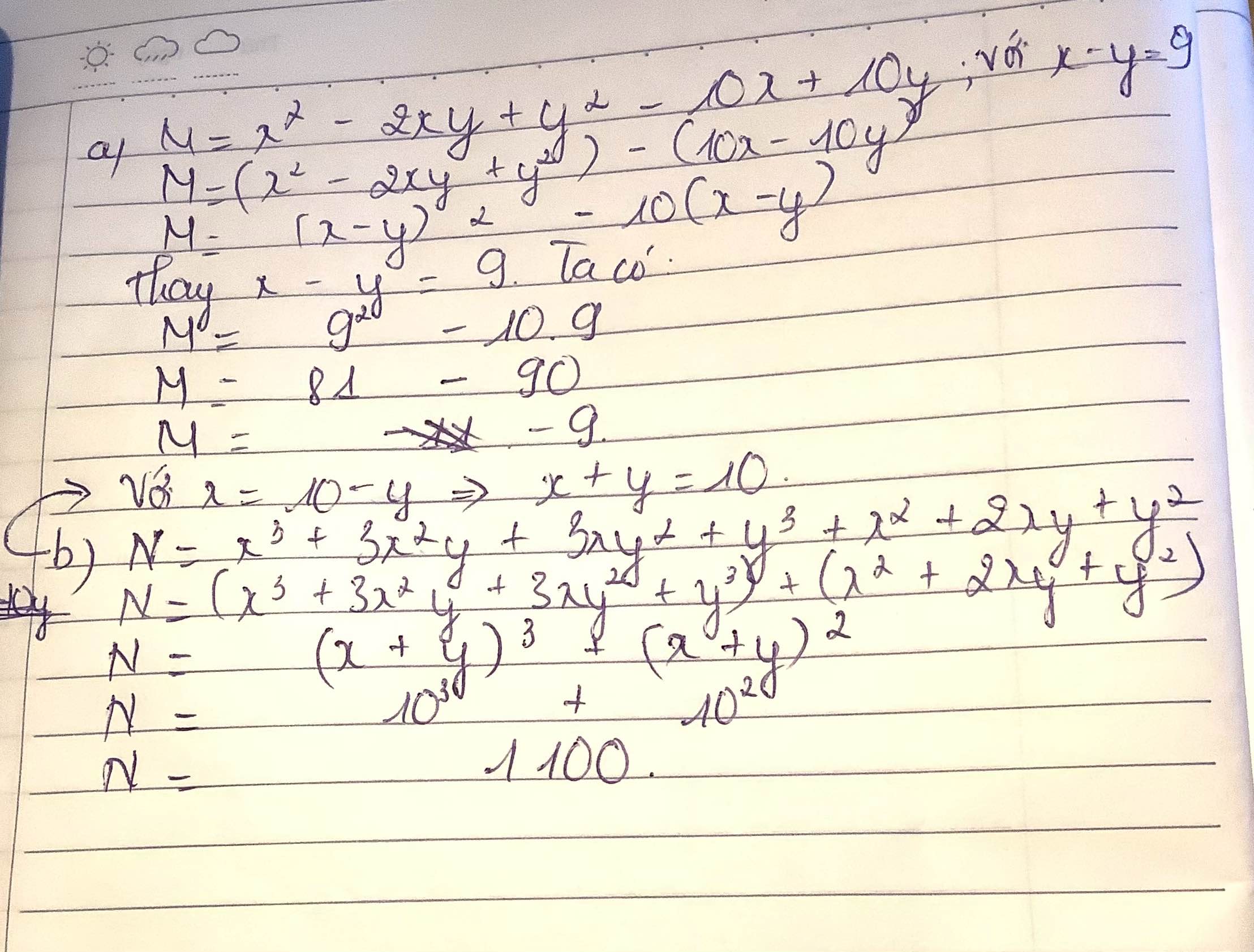x2+y2=(x+y)2-2xy hoặc (x-y)2+2xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(a,\left(-xy\right)\left(-2x^2y+3xy-7x\right)\)
\(=2x^3y^2-3x^2y^2+7x^2y\)
\(b,\left(\dfrac{1}{6}x^2y^2\right)\left(-0,3x^2y-0,4xy+1\right)\)
\(=-\dfrac{1}{20}x^4y^3-\dfrac{1}{15}x^3y^3+\dfrac{1}{6}x^2y^2\)
\(c,\left(x+y\right)\left(x^2+2xy+y^2\right)\)
\(=\left(x+y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3\)
\(d,\left(x-y\right)\left(x^2-2xy+y^2\right)\)
\(=\left(x-y\right)^3\)
\(=x^3-3x^2y+3xy^2-y^3\)
2.
\(a,\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
\(b,\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3+y^3\)
\(c,\left(4x-1\right)\left(6y+1\right)-3x\left(8y+\dfrac{4}{3}\right)\)
\(=24xy+4x-6y-1-24xy-4x\)
\(=\left(24xy-24xy\right)+\left(4x-4x\right)-6y-1\)
\(=-6y-1\)
#Toru

x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung

a: \(\dfrac{x^2+2xy+y^2}{x+y}=x+y\)
b: \(\dfrac{64x^3+1}{4x+1}=16x^2-4x+1\)

a) \(\left(x^2+2xy+y^2\right):\left(x+y\right)=\left(x+y\right)^2:\left(x+y\right)=x+y\)
b) \(=\left[\left(5x+1\right)\left(25x^2-5x+1\right)\right]:\left(5x+1\right)=25x^2-5x+1\)
c) \(=\left(y-x\right)^2:\left(y-x\right)=y-x\)
\(a,=\left(x+y\right)^2:\left(x+y\right)=x+y\\ b,=\left(5x+1\right)\left(25x^2-5x+1\right):\left(5x+1\right)=25x^2-5x+1\\ c,=\left(y-x\right)^2:\left(y-x\right)=y-x\)

b: (x-y)(x^2-2x+y)
\(=x^3-2x^2+xy-x^2y+2xy-y^2\)
\(=x^3-2x^2-x^2y+3xy-y^2\)
c: \(\left(x^2-y\right)\left(x+y^2\right)-\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3+x^2y^2-xy-y^3-\left(x^3-y^3\right)\)
\(=x^2y^2-xy\)
d: \(3x\left(2xy-z\right)-5y\left(x^2-2\right)+3xz\)
\(=6x^2y-3xz-5x^2y+10y+3xz\)
\(=x^2y+10y\)

a: \(\left(2x-1\right)^2-2\left(2x-3\right)^2+4\)
\(=4x^2-4x+1+4-2\left(4x^2-12x+9\right)\)
\(=4x^2-4x+5-8x^2+24x-18\)
\(=-4x^2+20x-13\)
e: \(\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)=8x^3+27y^3\)

1: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-\left(x^3+54\right)\)
\(=x^3+27-x^3-54\)
=-27
2: Ta có: \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=8x^3+y^3-8x^3+y^3\)
\(=2y^3\)
\(1,=x^3+270-x^3-54=-27\\ 2,=8x^3+y^3-8x^3+y^3=2y^3\\ 3,=x^3-3x^2+3x-1-x^3-8+3x^2-48=3x-57\\ 4,=x^3-x-x^3-1=-x-1\\ 5,=8x^3-5\left(8x^3+1\right)=-32x^3-5\\ 6,=27+x^3-27=x^3\\ 7,làm.ở.câu.3\\ 8,=x^3-6x^2+12x-8+6x^2-12x+6-x^3-1+3x\\ =3x-3\)

a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)