làm câu c và vẽ hình thôi ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CB
hình ko cần vẽ đâu ạ, em vẽ rồi. Làm giúp em câu 2b thôi
1
NH
làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ
1
25 tháng 10 2023
10: Chọn B
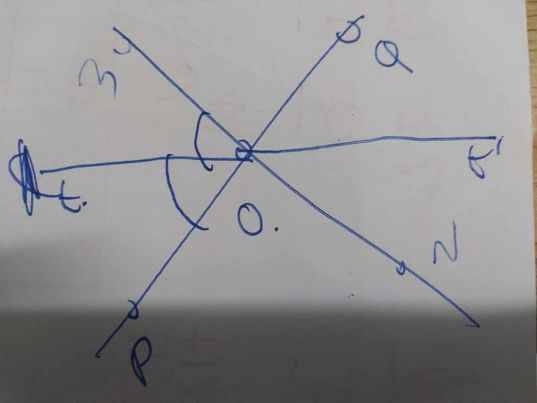
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
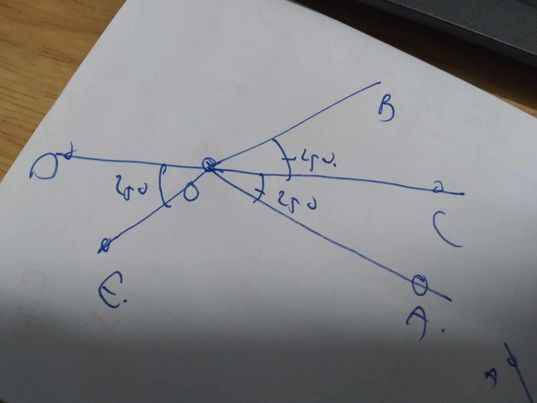
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
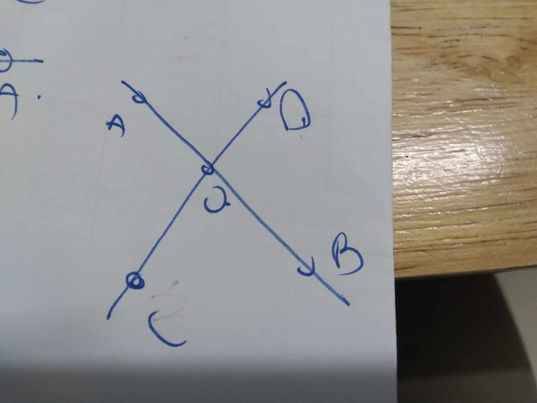
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B
3B
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
1
15 tháng 5 2023
a: góc AMB=1/2*180=90 độ
góc AMN+góc AKN=180 độ
=>AMNK là tứ giác nội tiếp
b: ΔCAB vuông tại A có AM vuông góc CB
nên CA^2=MC*CB
TL
1
10 tháng 12 2021
Bài 11:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔCDA có
P là trung điểm của CD
Q là trung điểm của DA
Do đó: PQ là đường trung bình của ΔCDA
Suy ra: PQ//AC và PQ=AC/2(2)
Từ (1) và (2) suy raMN//PQ và MN=PQ
hay MNPQ là hình bình hành
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
KL
1
AP
11 tháng 10 2021
uses crt;
var a:array[1..100] of integer;
i,n,d,tong :integer;
begin
clrscr;
d:=0;
tong:=0;
readln(n);
for i:=1 to n do
readln(a[i]);
end;
for i:=1 to n do
if (a[i]>0) then begin
d:=d+1;
if d=1 then begin writeln('trong day co so nguyen duong '); write(' vi tri cua cac so duong ',i); end
else
begin
tong:=tong+a[i];
write(' ',i);
end;
end
else if ((i=n)and(d=0)) then write(' khong co so duong');
writeln;
writeln(' tong so luong so nguyen duong trong day so: ',d);
writeln(' ton cac so nguyen duong: ',tong);
readln;
end.
QM
0
BN
2
11 tháng 5 2021
Bài 5:
a) Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABM=ΔEBM(cạnh huyền-góc nhọn)
11 tháng 5 2021
Bài 5:
b) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc ở đáy)
\(\Leftrightarrow\widehat{MCB}+60^0=90^0\)
hay \(\widehat{MCB}=30^0\)(1)
Ta có: BM là tia phân giác của \(\widehat{ABC}\)(gt)
nên \(\widehat{MBC}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(Định lí đảo của tam giác cân)
Suy ra: MB=MC(Hai cạnh bên)
Xét ΔMBE vuông tại E và ΔMCE vuông tại E có
MB=MC(cmt)
ME chung
Do đó: ΔMBE=ΔMCE(cạnh huyền-cạnh góc vuông)
Suy ra: BE=CE(Hai cạnh tương ứng)
TH
0