Cho x,y > 0 vì x + y = 2
CMR: x2y2 (x2+y2) bé hơn hoặc bằng 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CD
1
Những câu hỏi liên quan
NV
1
NN
1
12 tháng 6 2023
Với x, y là hai số dương, dễ dàng chứng minh x + y 2,
do x + y = 2 => 0 < xy ≤ 1 (1)
Ta lại có: 2xy( x2 + y2) ≤
=> 0 < 2xy(x2 + y2) ≤ (x+y)4/4 = 4
=> 0 < xy( x2 + y2) ≤ 2 (2)
Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)
Dấu “=” xảy ra khi x = y = 1
KN
22 tháng 2 2020
Áp dụng bđt Cauchy - Schwarz dạng Engel, ta được:
\(\frac{1}{x}+\frac{1}{y}\ge\frac{\left(1+1\right)^2}{x+y}=\frac{4}{x+y}\)
Dấu "=" xảy ra khi \(x=y=\frac{1}{2}\)
KN
22 tháng 2 2020
Thật ra bài này không cần điều kiện \(x+y\le1\)thì \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)vẫn đúng với x,y dương và x = y.
Mình nghĩ nên chứng minh \(\frac{1}{x}+\frac{1}{y}\ge4\)thì điều kiện \(x+y\le1\) sẽ có nghĩa!
28 tháng 3 2021
xí câu 1:))
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{x^2}{y-1}+\frac{y^2}{x-1}\ge\frac{\left(x+y\right)^2}{x+y-2}\)(1)
Đặt a = x + y - 2 => a > 0 ( vì x,y > 1 )
Khi đó \(\left(1\right)=\frac{\left(a+2\right)^2}{a}=\frac{a^2+4a+4}{a}=\left(a+\frac{4}{a}\right)+4\ge2\sqrt{a\cdot\frac{4}{a}}+4=8\)( AM-GM )
Vậy ta có đpcm
Đẳng thức xảy ra <=> a=2 => x=y=2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 6 2020
Đặt \(\left(\frac{yz}{x};\frac{zx}{y};\frac{xy}{z}\right)=\left(a;b;c\right)\Rightarrow ab+bc+ca=x^2+y^2+z^2=3\)
Ta có:
\(a+b+c\ge\sqrt{3\left(ab+bc+ca\right)}=\sqrt{9}=3\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\) hay \(x=y=z=1\)
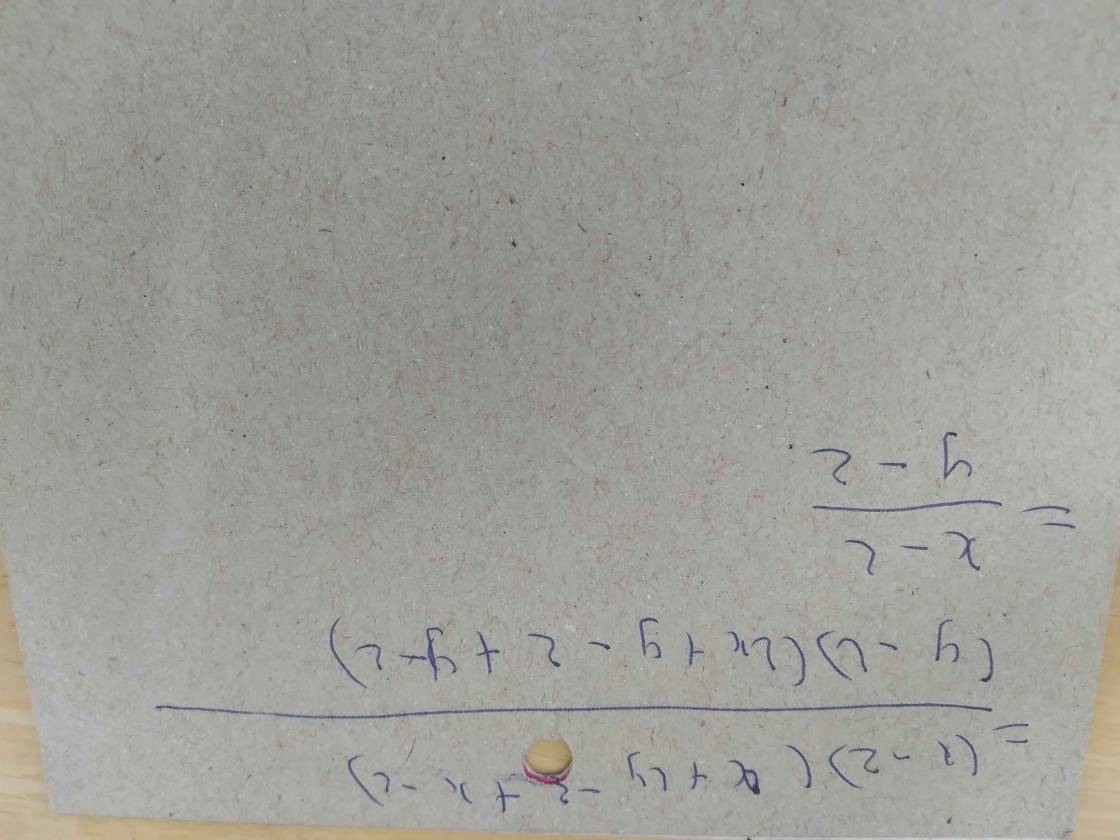
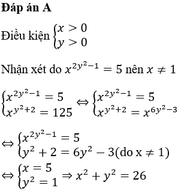
\(Gt\Rightarrow\left(x+y\right)^2=4\Rightarrow x^2+2xy+y^2=4\Rightarrow x^2+y^2=4-2xy\)
\(\Rightarrow x^2y^2\left(x^2+y^2\right)=x^2y^2\left(4-2xy\right)\)
Ta cần CM:\(x^2y^2\left(4-2xy\right)\le2\Leftrightarrow x^2y^2\left(2-1xy\right)\le1\)
\(\Leftrightarrow x^3y^3-2x^2y^2+1\ge0\)
\(\Leftrightarrow\left(xy-1\right)\left(x^2y^2-xy-1\right)\ge0\)
\(\Leftrightarrow\left(xy-1\right)\left[xy\left(xy-1\right)-1\right]\ge0\)
Áp dụng BĐT Cô-si ta lại có \(2=x+y\ge2\sqrt{xy}\)
\(\Rightarrow xy\le1\Rightarrow xy-1\le0\)
\(xy>0\Rightarrow xy\left(xy-1\right)\le0\Rightarrow xy\left(xy-1\right)-1\le-1\)
\(\Rightarrow\left(xy-1\right)\left[xy\left(xy-1\right)-1\right]\ge0\)luôn đúng do tích của 2 số âm thì luôn\(\ge\)0
Dấu " = " xảy ra <=> xy = 1 ; x = y và x + y = 2 <=> x = y = 1