cho một tam giác ABC vuông tại A; tia phân giác của góc B cắt AC ở D. So sánh các độ dài AD;DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
28 tháng 7 2023
Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.
b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.
Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.
b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.
AF
23 tháng 9 2020
Bài giải
A B C D 1 2 1
Vì \(\Delta ABC\) vuông cân tại A nên \(\widehat{B_1}=\widehat{C_1}=\left(180^o-90^o\right)\text{ : }2=45^o\)
Vì \(\Delta BCD\) vuông cân tại B nên \(\widehat{D}=\widehat{C_2}=\left(180^o-90^o\right)\text{ : }2=45^o\)
\(\Rightarrow\text{ }\widehat{B_1}=\widehat{C_2}\left(=45^o\right)\) nên \(AB\text{ }//\text{ }CD\)
\(\Rightarrow\text{ Tứ giác ABCD là hình thang}\)
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
CM
30 tháng 7 2018
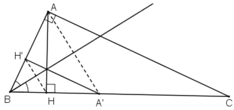
Gọi d là đường phân giác của góc B của ΔABC.
+ Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC; biến B thành B
(Dễ dàng nhận thấy H’ ∈ BA; A’ ∈ BC).
⇒ ΔH’BA’ = Đd(ΔHBA).
⇒ ΔH’BA’ = ΔHBA.
Mà ΔABC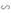 
ΔHBA theo tỉ số 
⇒ ΔABC 
ΔH’BA’ theo tỉ số k
⇒ AB = k.H’B; BC = k.BA’.
Mà A ∈ tia BH’ ; C ∈ tia BA’
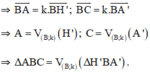
Vậy phép đồng dạng cần tìm là phép vị tự tâm B, tỉ số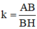 
hợp với phép đối xứng trục d là phân giác của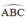 
11 tháng 10 2021
Bài 1:
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AB=\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{6}{7}\)
nên \(\widehat{B}=59^0\)
hay \(\widehat{C}=31^0\)
9 tháng 2 2021
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BC^2+AB^2\)
\(\Leftrightarrow AB^2=AC^2-BC^2=12^2-8^2=80\)
hay \(AB=4\sqrt{5}cm\)
Vậy: \(AB=4\sqrt{5}cm\)
Bài 2:
Áp dụng định lí Pytago vào ΔMNP vuông tại N, ta được:
\(MP^2=MN^2+NP^2\)
\(\Leftrightarrow MN^2=MP^2-NP^2=\left(\sqrt{30}\right)^2-\left(\sqrt{14}\right)^2=16\)
hay MN=4cm
Vậy: MN=4cm
9 tháng 2 2021
Bài 1 :
- Áp dụng định lý pi ta go ta được :\(BA^2+BC^2=AC^2\)
\(\Leftrightarrow AB^2+8^2=12^2\)
\(\Leftrightarrow AB=4\sqrt{5}\) ( cm )
Vậy ...
Bài 2 :
- Áp dụng định lý pi ta go vào tam giác MNP vuông tại N có :
\(MN^2+NP^2=MP^2\)
\(\Leftrightarrow MN^2+\sqrt{14}^2=\sqrt{30}^2\)
\(\Leftrightarrow MN=4\) ( đvđd )
Vậy ...
Lời giải:
Kẻ $DK\perp BC$. Xét tam giác $BAD$ và $BKD$ có:
$\widehat{BAD}=\widehat{BKD}=90^0$
$\widehat{ABD}=\widehat{KBD}$ (do $BD$ là tia phân giác $\widehat{B}$)
$BD$ chung
$\Rightarrow \triangle BAD=\triangle BKD$ (ch-gn)
$\Rightarrow AD=DK$
Mà $DK<DC$ (do trong tam giác vuông $DKC$ thì cạnh góc vuông $DK$ luôn nhỏ hơn cạnh huyền $DC$)
$\Rightarrow AD< DC$
Hình vẽ: