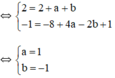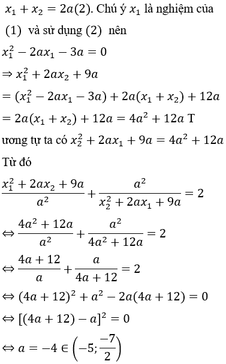Cho hàm số y = ax2 a, ( 2;2 ) b, vẽ đồ thị hàm số với giá trị a vừa tìm được?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 2 2022
a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
17 tháng 2 2022
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1
CM
19 tháng 7 2017
Ta có
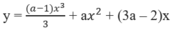
y' = (a - 1) x 2 + 2ax + 3a - 2.
Với a = 1, y' = 2x + 1 đổi dấu khi x đi qua -1/2. Hàm số không đồng biến.
Với a ≠ 1 thì với mọi x mà tại đó y' ≥ 0
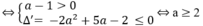
(y' = 0 chỉ tại x = -2, khi a = 2).
Vậy với a ≥ 2 hàm số luôn đồng biến
CM
22 tháng 6 2019
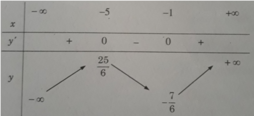
Khi a = 3/2 thì
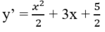
y' = 0 ⇔ x 2 + 6x + 5 = 0 ⇔ x = -1 hoặc x = -5.
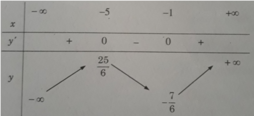
Đồ thị như trên Hình 1.18
Vì
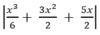
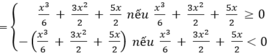
nên từ đồ thị (C) ta suy ngay ra đồ thị của hàm số
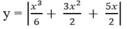
như trên Hình 1.19
30 tháng 7 2023
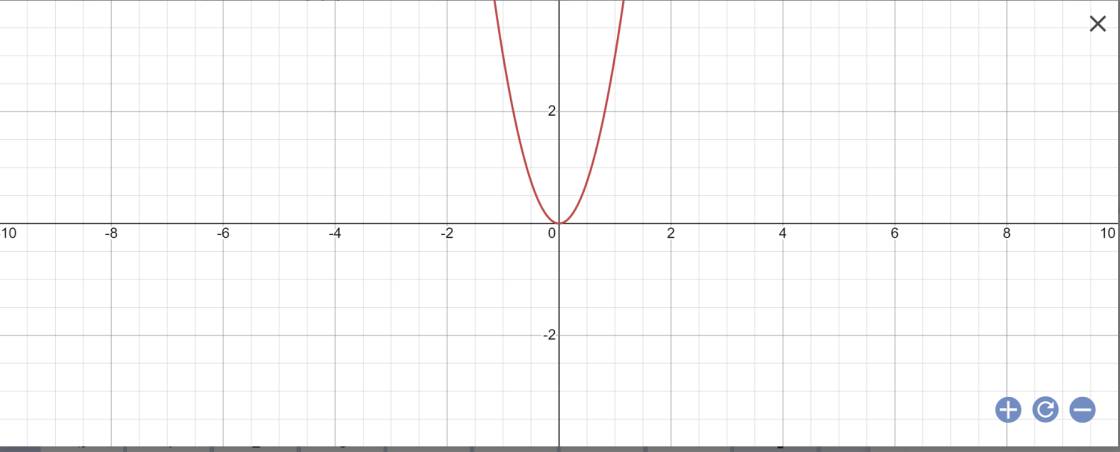
a: Thay x=-1 và y=3 vào (P), ta được:
a*(-1)^2=3
=>a=3
b: y=3x^2
CM
11 tháng 6 2018
Đáp án A
Ta có y ' = x 2 − 2 a x − 3 a . Để hàm số đặt cực trị tại x 1 , x 2
thì Δ ' = a 2 + 3 a > 0 ⇔ a > 0 a < − 3
Khi đó
x 1 + x 2 = 2 a x 1 x 2 = − 3 a ⇒ x 1 2 + 2 a x 2 + 9 a = x 1 2 + x 1 + x 2 x 2 − 3 x 1 x 2 = x 1 + x 2 2 − 4 x 1 x 2 = 4 a 2 + 12 a
Tương tự ta cũng có x 2 2 + 2 a x 1 + 9 a = 4 a 2 + 12 a . Từ đó suy ra
x 1 2 + 2 a x 2 + 9 a a 2 + a 2 x 2 2 + 2 a x 1 + 9 a = 4 a + 12 a + a 4 a + 12 = 2 ⇔ a 4 a + 12 = 1 ⇔ a = − 4
