Ai trình bày giúp mình cách tìm công thức số hạng tổng quát của 2 câu này với ạ, mình xin cảm ơn ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 7 2016
mik chỉ bít quy luật của dãy thôi,nó là:
số hạng thứ nhất là 2,số hạng thứ 2 thì cộng thêm 3,tiếp theo +(3+2), sau nữa +(3+2+2),......
mong là câu trả lời này có thể giúp bạn!chúc bạn học tốt!
H
5 tháng 4 2021
Để làm dạng này , bạn làm như sau :
Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là
Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95
Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.
Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.
Bạn điền 57 vào phần chỗ chấm trước giây.
Vậy 0,8325 giờ=49 phút 57 giây
MN
3 tháng 4 2021
Câu 1
Trong số các chất có công thức hoá học dưới đây, chất nào làm quì tím hoá xanh:
A. Dung dịch HCl |
B. Cu |
C. Dung dịch NaOH |
D. H2O |
Câu 2
Khí H2 cháy trong khí O2 tạo nước theo phản ứng:
H2 + O2 to H2O
Muốn thu được 5,4g nước thì thể tích khí H2 (đktc) đã đốt là:
A. 2,24lít |
B. 6,72lít |
C. 4,48lít |
D. 1,12lít |
Câu 3
Kim loại không tan trong nước là:
A. Cu |
B. K |
C. Na |
D. Ba |
Câu 4
Trong số các chất có công thức hoá học dưới đây, chất nào làm quì tím hoá đỏ:
A. Dung dịch HCl |
B. H2O |
C. Cu |
D. Dung dịch NaOH |
Câu 5
Đốt cháy pirit sắt FeS2 trong khí oxi, phản ứng xảy ra theo phương trình:
FeS2 + O2 to Fe2O3 + SO2
Sau khi cân bằng hệ số của các chất là phương án nào sau đây?
A. 4, 11, 2, 8 |
B. 4, 12, 2, 6 |
C. 2, 3, 2, 4 |
D. 4, 10, 3, 7 |
Câu 6
Dãy gồm các kim loại tác dụng với nước ở nhiệt độ thường là
A. Fe, Cu, Ag. |
B. Zn, Al, Ag |
C. Fe, Mg, Al. |
D. Na, K, Ca. |
Câu 7
Phản ứng nào dưới đây không phải là phản ứng thế?
A. Ca(OH)2 + CO2 → CaCO3 +H2O |
B. Mg +2HCl → MgCl2 +H2 |
C. Zn + CuSO4 → ZnSO4 +Cu |
D. Zn + H2SO4 → ZnSO4 + H2 |
Câu 8
Cho Zn tác dụng với dung dịch axit HCl sẽ có hiện tượng sau:
1. Kẽm tan
2. Sủi bọt khí
3. Không hiện tượng
A. 3 |
B. 1 |
C. 2 |
D. 1 và 2 |
Câu 9
Cho 48g CuO tác dụng với khí H2 khi đun nóng, thể tích khí H2 ( đktc) cho phản ứng trên là:
A. 13,88 lít |
B. 14,22 lít |
C. 11,2 lít |
D. 13,44 lít |
Câu 10
Gốc axit của axit HNO3 hóa trị mấy?
A. I |
B. IV |
C. II |
D. III |
PQ
2
N
19 tháng 10 2021
Bài 3:
a. \(R=R1+R2=15+30=45\Omega\)
b. \(\left\{{}\begin{matrix}I=U:R=9:45=0,2A\\I=I1=I2=0,2A\left(R1ntR2\right)\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}U1=R1.I1=15.0,2=3V\\U2=R2.I2=30.0,2=6V\end{matrix}\right.\)
Bài 4:
\(I1=U1:R1=6:3=2A\)
\(\Rightarrow I=I1=I2=2A\left(R1ntR2\right)\)
\(U=R.I=\left(3+15\right).2=36V\)
\(U2=R2.I2=15.2=30V\)
HT
29 tháng 4 2021
22/ \(\omega A=8\pi\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow A^2=3,2^2+\dfrac{\left(4,8\pi\right)^2}{\omega^2}\)
\(\Leftrightarrow\omega^2A^2=3,2^2\omega^2+23,04\pi^2\Leftrightarrow64\pi^2=3,2^2.\omega^2+23,04\pi^2\Leftrightarrow\omega=2\pi\left(rad/s\right)\)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{2\pi}{2\pi}=1\left(Hz\right)\Rightarrow D.1Hz\)
23/ \(\omega A=20;\omega^2A=80\Rightarrow\left\{{}\begin{matrix}\omega=4\left(rad/s\right)\\A=5cm\end{matrix}\right.\)
\(\Rightarrow v=\omega\sqrt{A^2-x^2}=4.\sqrt{5^2-4^2}=12\left(cm/s\right)\Rightarrow A.12cm/s\)
NP
2
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m
TM
6 tháng 4 2023
Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
TM
6 tháng 4 2023
Bài IV.b.
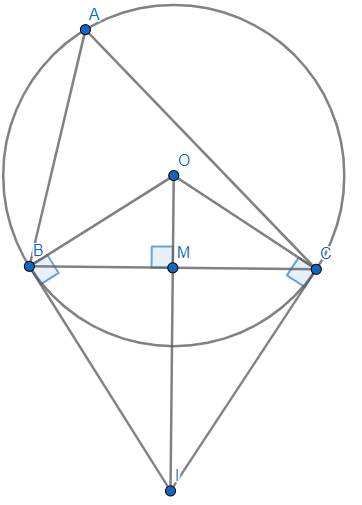
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
4.
\(u_{n+1}=\dfrac{u_n}{3u_n+1}\Rightarrow\dfrac{1}{u_{n+1}}=\dfrac{3u_n+1}{u_n}=\dfrac{1}{u_n}+3\)
Đặt \(\dfrac{1}{u_n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{u_1}=2\\v_{n+1}=v_n+3\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số cộng với công bội \(d=3\)
\(\Rightarrow v_n=v_1+\left(n-1\right)d=2+3\left(n-1\right)=3n-1\)
\(\Rightarrow u_n=\dfrac{1}{v_n}=\dfrac{1}{3n-1}\)
6.
\(u_{n+1}=4u_n-3u_{n-1}\Leftrightarrow u_{n+1}-u_n=3\left(u_n-u_{n-1}\right)\)
Đặt \(u_{n+1}-u_n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_2-u_1=3\\v_n=3v_{n-1}\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số nhân với công bội \(q=3\)
\(\Rightarrow v_n=3.3^{n-1}=3^n\)
\(\Rightarrow u_{n+1}-u_n=3^n\)
\(\Rightarrow u_{n+1}-\dfrac{1}{2}.3^{n+1}=u_n-\dfrac{1}{2}.3^n\)
Đặt \(u_n-\dfrac{1}{2}.3^n=x_n\Rightarrow\left\{{}\begin{matrix}x_1=u_1-\dfrac{1}{2}.3^1=-\dfrac{1}{2}\\x_{n+1}=x_n\end{matrix}\right.\)
\(\Rightarrow x_{n+1}=x_n=x_{n-1}=...=x_1=-\dfrac{1}{2}\)
\(\Rightarrow u_n-\dfrac{1}{2}.3^n=-\dfrac{1}{2}\Rightarrow u_n=\dfrac{3^n-1}{2}\)