Xác định các hệ số a, b,c để:
(x2+cx+2)(ax+b)=x3-x2+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ta được
CM
18 tháng 11 2018
a và b thỏa mãn hệ phương trình :
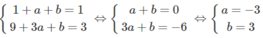
c và d thỏa mãn hệ phương trình:
N
2
22 tháng 3 2016
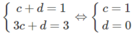
Phân tích đa thức x2+ x-6 = (x-2)(x+3)
Gọi thương của phép chia f(x) cho đa thức trên là Q(x)
Ta có f(2)= 8+ 2a+b=0
Suy ra 2a+b=-8
lại có f(-3)= -27+ 3a+b=0
Suy ra 3a+b=27
đến đây ta dùng máy tính giải hệ ta được a=35;b=-78
DK
1
17 tháng 6 2016
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
HL
0
YN
0
\(\left(x^2+cx+2\right)\left(ax+b\right)=x^3-x^2+2\)
\(\Leftrightarrow x^3a+x^2b+x^2ac+xbc+2xa+2b=x^3-x^2+2\)
\(\Leftrightarrow x^3a+\left(b+ac\right)x^2+\left(bc+2a\right)x+2b=x^3-x^2+2\)
\(\Leftrightarrow\hept{\begin{cases}x^3a=x^3\\\left(b+ac\right)x^2=-x^2\\\left(bc+2a\right)x=0\end{cases}}\)
2b=2
\(\Leftrightarrow\hept{\begin{cases}a=1\\ac+b=-1\\2a+bc=0\end{cases}}\)
b=1
\(\Leftrightarrow\hept{\begin{cases}a=1\\1.c+b=c+b=-1\\2.1+1.c=2+c=0\end{cases}}\)
b=1
\(\Leftrightarrow\hept{\begin{cases}a=1\\c=-2\\c=1\end{cases}}\)