giúppppp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 3 2023
a: \(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2021}{2022}=\dfrac{1}{2022}\)
b: \(=\dfrac{2\left(\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}\right)}{11\left(\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}\right)}=\dfrac{2}{11}\)
Y
25 tháng 3 2023
Chiều rộng hình chữ nhật là :
\(\dfrac{17}{2}:3=\dfrac{17}{6}\left(cm\right)\)
Diện tích hình chữ nhật là :
\(\dfrac{17}{6}.\dfrac{17}{2}=\dfrac{289}{12}\approx24\left(cm^2\right)\)
H
21 tháng 4 2021
\(a) Fe + 2HCl \to FeCl_2 + H_2\\ b) n_{Fe} = n_{H_2} = \dfrac{2,24}{22,4} = 0,1(mol)\\ m_{Fe} = 0,1.56 = 5,6(gam)\\ n_{Cu} = 12-5,6 = 6,4(gam)\)
1 tháng 4 2019
\(220-\frac{b}{b}=\frac{4}{7}\)
\(\Leftrightarrow\frac{b}{b}=220-\frac{4}{7}\)
\(\Leftrightarrow\frac{b}{b}=\frac{1536}{7}\)
\(\Leftrightarrow b\)không tồn tại nghiệm số thực
\(\Leftrightarrow b\in\varnothing\)
PT
1
TT
Trần Thị Khiêm
VIP
2 giờ trước (8:31)
Đề:
Cho tam giác nhọn \(A B C\), các đường cao \(A D , B E , C F\) đồng quy tại trực tâm \(H\).
Lấy \(X \in A D , Y \in B E , Z \in C F\) sao cho
\(\frac{D X}{D A} + \frac{E Y}{E B} + \frac{F Z}{F C} = 1.\)
Chứng minh \(H , X , Y , Z\) cùng thuộc một đường tròn.
Ý tưởng giải
Điều kiện “tổng tỉ lệ = 1” gợi đến Định lý Ceva dạng lượng giác hay dạng tỷ số đoạn thẳng. Nhưng ở đây lại liên quan đến tính chất hàng điểm điều hòa và lực của điểm (power of a point).
Một hướng quen thuộc: chứng minh rằng
\(\frac{D X}{D A} = \frac{H D}{H A} , \frac{E Y}{E B} = \frac{H E}{H B} , \frac{F Z}{F C} = \frac{H F}{H C} .\)
Nếu thay vào, điều kiện đề bài trở thành
\(\frac{H D}{H A} + \frac{H E}{H B} + \frac{H F}{H C} = 1.\)
Mà đẳng thức này đúng với trực tâm \(H\) trong tam giác nhọn (một đẳng thức quen thuộc trong hình học tam giác). Đây là chìa khoá.
Các bước chứng minh
- Biểu diễn điều kiện bằng lực của điểm H:
Trên đoạn \(A D\), nếu \(X\) thỏa
\(\frac{D X}{D A} = \frac{H D}{H A} ,\)
thì theo định nghĩa, ta có
\(H X \cdot H A = H D \cdot D A .\)
Nghĩa là \(H\) và \(A , D , X\) đồng viên.
Tương tự trên \(B E , C F\). - Từ đó ta suy ra \(H\) nằm trên các đường tròn \(\left(\right. A , D , X \left.\right) , \left(\right. B , E , Y \left.\right) , \left(\right. C , F , Z \left.\right)\).
- Giao của ba đường tròn này chính là điểm \(H\).
Mặt khác, nhờ điều kiện tổng bằng 1, ba đường tròn này cùng đi qua một điểm thứ hai (không phải \(H\)). Chính là điểm chung của ba đường tròn – đó là đường tròn đi qua \(H , X , Y , Z\). - Do đó, bốn điểm \(H , X , Y , Z\) đồng viên.
✅ Kết luận:
\(H , X , Y , Z \&\text{nbsp};\text{c} \overset{ˋ}{\text{u}} \text{ng}\&\text{nbsp};\text{thu}ộ\text{c}\&\text{nbsp};\text{m}ộ\text{t}\&\text{nbsp};đườ\text{ng}\&\text{nbsp};\text{tr} \overset{ˋ}{\text{o}} \text{n}.\)
NK
Nguyễn KIm Ngân
VIP
1 giờ trước (8:46)
Khi đó, ta có các vector vị trí sau:
- Vector a, b, c lần lượt là vector vị trí của A, B, C.
- Vector m=2b+c là vector vị trí của trung điểm M của BC.
- Vector n=2c+a là vector vị trí của trung điểm N của CA.
- Vector p=2a+b là vector vị trí của trung điểm P của AB.
Đường thẳng thứ nhất đi qua M và song song với OA (tức là song song với vector a). Phương trình vector của đường thẳng này là: dM:r=m+t1a=2b+c+t1a
Đường thẳng thứ hai đi qua N và song song với OB (tức là song song với vector b). Phương trình vector của đường thẳng này là: dN:r=n+t2b=2c+a+t2b
Đường thẳng thứ ba đi qua P và song song với OC (tức là song song với vector c). Phương trình vector của đường thẳng này là: dP:r=p+t3c=2a+b+t3c
Để chứng minh ba đường thẳng này đồng quy, ta cần tìm một điểm chung. Giả sử điểm đồng quy đó là K. Vector vị trí của K là k.
Nếu K là giao điểm của dM và dN, ta có: 2b+c+t1a=2c+a+t2b 2b+2c+t1a=2c+2a+t2b t1a−2a+2b−t2b=0 (t1−21)a+(21−t2)b=0 Do a và b là các vector không cùng phương (A, B, O không thẳng hàng), nên đẳng thức trên chỉ xảy ra khi các hệ số bằng 0. t1−21=0⟹t1=21 21−t2=0⟹t2=21
Thay t1=21 vào phương trình dM, ta được vector vị trí của giao điểm K: k=2b+c+21a=2a+b+c
Bây giờ ta kiểm tra xem điểm K này có thuộc đường thẳng dP không. Ta cần tìm t3 sao cho: k=2a+b+t3c 2a+b+c=2a+b+t3c 2a+b+2c=2a+b+t3c 2c=t3c Vì c=0, ta suy ra t3=21.
Vì tồn tại giá trị t3=21 sao cho K thuộc đường thẳng dP, nên điểm K nằm trên cả ba đường thẳng. Do đó, ba đường thẳng đã cho đồng quy tại một điểm có vector vị trí là k=2a+b+c.
Đây chính là trọng tâm của tam giác ABC, cũng chính là tâm đường tròn Euler của tam giác.
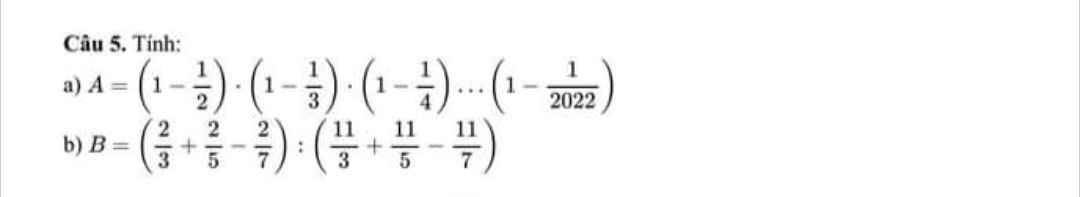
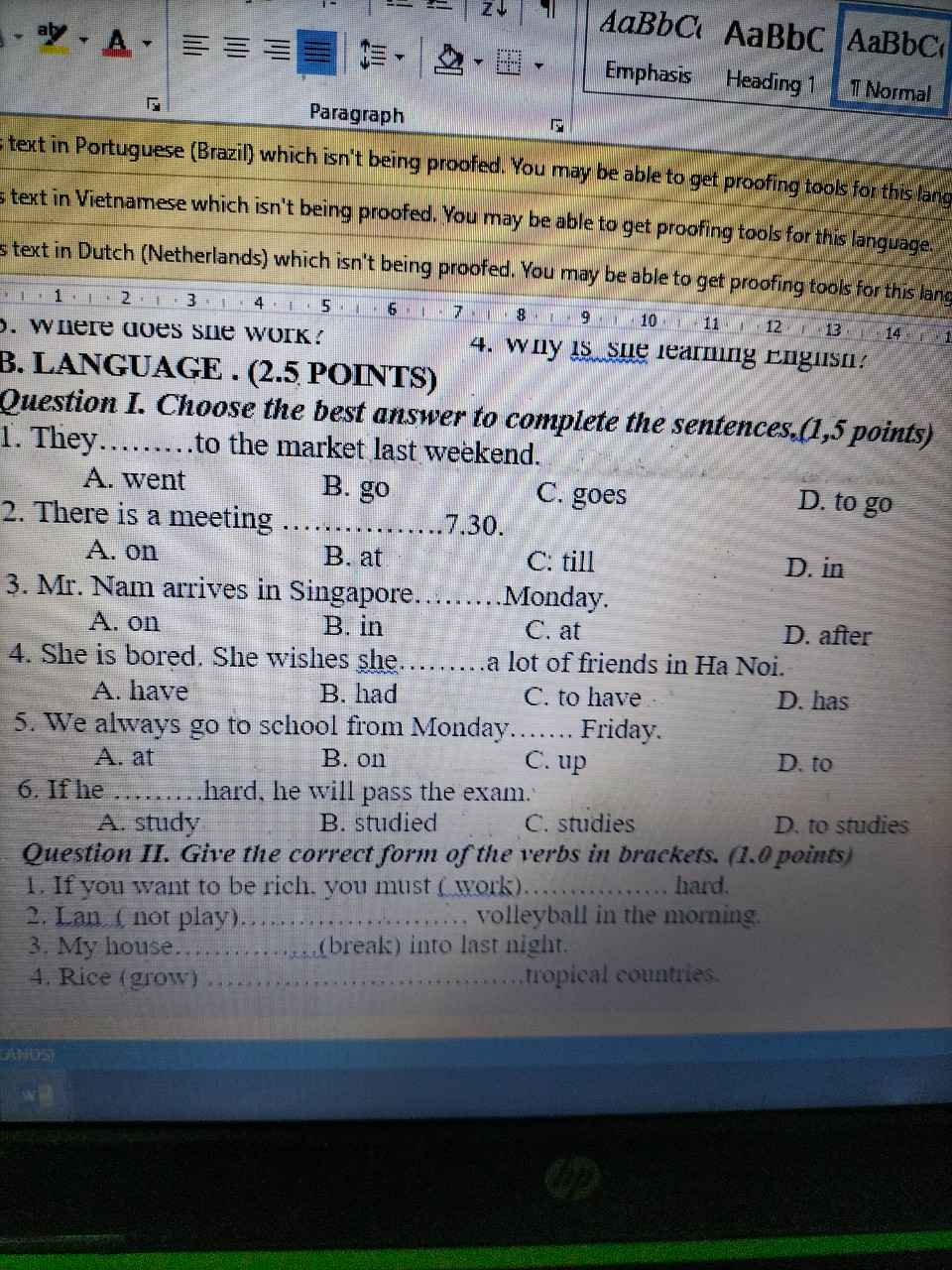
Tham khảo:
CHÚC EM HỌC TỐT NHÉ
Cop mạng hay là tự lm vậy bn