 giúp mình ạ
giúp mình ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2.16\ge2^n>4\)
\(2.2^4\ge2^n>2^2\)
\(2^5\ge2^n>2^2\)
=> \(n\in\left\{3,4,5\right\}\)
Vậy: \(n\in\left\{3,4,5\right\}\)



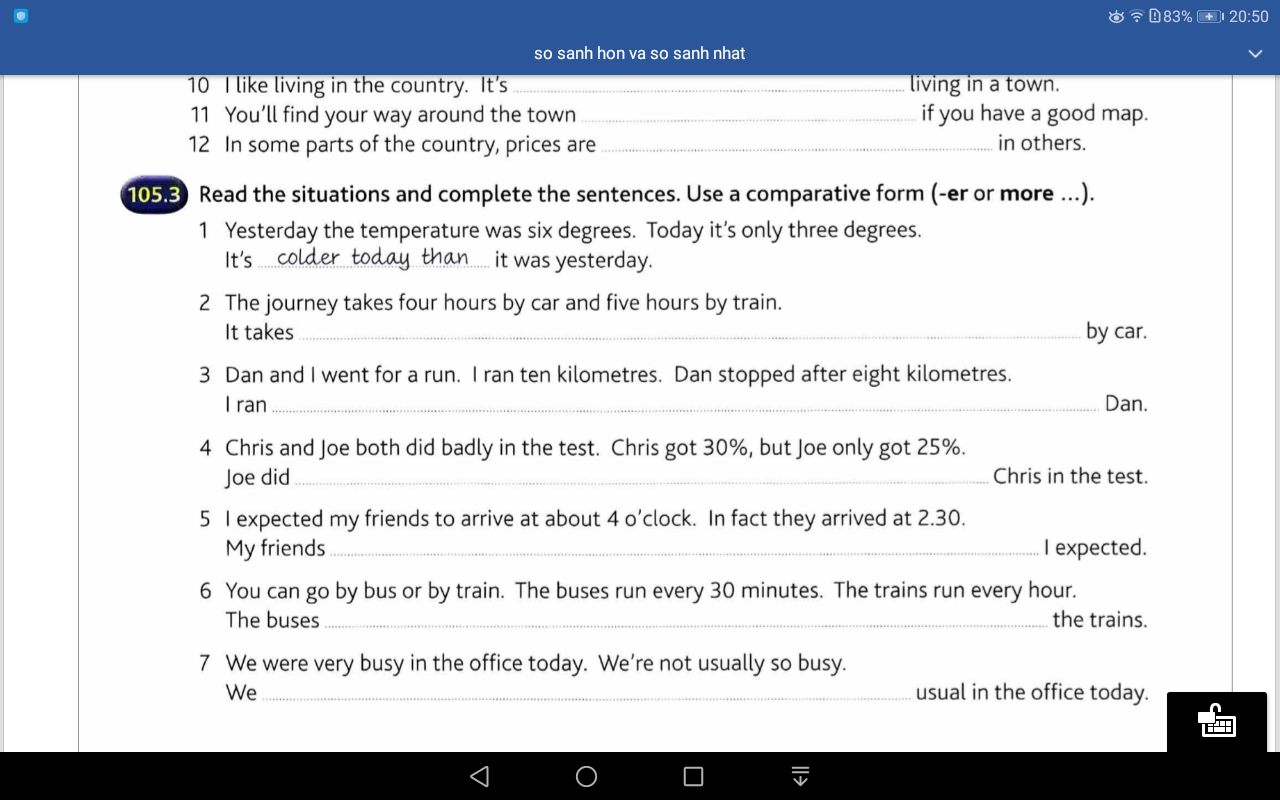
2 It take more hours to travel by train than to travel
6 The bus run more frequently than the trains



303.(bài này làm ở dưới kia rồi)
304. a, K1,K2 mở =>R1 nt R2 \(=>Rtd=R1+R2=4\Omega\)
b, K1 mở, K2 đóng =>(R1 nt R2)//R5
\(=>Rtd=\dfrac{R5\left(R1+R2\right)}{R5+R1+R2}=2\Omega\)
c,K1 đóng,K2 mở=>R2 nt {R1//(R3 nt R4)}
\(=>Rtd=R2+\dfrac{R1\left(R3+R4\right)}{R1+R3+R4}=3,875\Omega\)
d, K1,K2 đóng =>R5 //{R2 nt {R1//(R3 nt R4)}}
\(=>Rtd=\dfrac{R5\left\{R2+\dfrac{R1\left(R3+R4\right)}{R1+R3+R4}\right\}}{R5+R2+\dfrac{R1\left(R3+R4\right)}{R1+R3+R4}}=.....\)(thay số vào tính)

\(a.Thayx=-3:A=\left(-3\right)^2-2.\left(-3\right)+3.\\ =9+6+3=18.\)
\(b.Thay\) \(x=m;A=3:\)
\(3=m^2-2m+3.\\ \Leftrightarrow m^2-2m=0.\\ \Leftrightarrow\left[{}\begin{matrix}m=0.\\m=2.\end{matrix}\right.\)
Bài 1:
a, Biểu thức tính quãng đường đi được trong a giờ đầu tiên là: 40a
Biểu thức tính quãng đường AB là: 40a+50b
Bài 2:
a, Thay x=-3 vào A ta có:
\(A=x^2-2x+3=\left(-3\right)^2-2\left(-3\right)+3=9+6+3=18\)
b, Thay x=m, A=3 ta có:
\(m^2-2m+3=3\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)

a) Xét \(\Delta ABC\) cân tại A:
AH là đường cao (gt).
\(\Rightarrow\) AH là đường phân giác \(\widehat{BAC}\) (T/c tam giác cân).
\(\Rightarrow\widehat{BAH}=\widehat{CAH}.\)
b) Xét \(\Delta ABC\) cân tại A:
AH là đường cao (gt).
\(\Rightarrow\) AH là đường trung tuyến (T/c tam giác cân).
\(\Rightarrow\) H là trung điểm của BC.
Xét \(\Delta ABC:\)
H là trung điểm của BC (cmt).
\(HI//AB\left(gt\right).\)
\(\Rightarrow\) I là trung điểm của AC.
Xét \(\Delta ABC:\)
I là trung điểm của AC (cmt).
H là trung điểm của BC (cmt).
\(\Rightarrow\) IH là đường trung bình.
\(\Rightarrow\) \(IH=\dfrac{1}{2}AB\) (T/c đường trung bình).
Mà \(AB=AC(\Delta ABC\) cân tại A\().\)
\(IC=\dfrac{1}{2}AC\) (I là trung điểm của AC).
\(\Rightarrow IH=IC.\)
\(\Rightarrow\Delta IHC\) cân tại I.



 chỉ giúp mình bài 303 với ạ mình cần gấp
chỉ giúp mình bài 303 với ạ mình cần gấp

\(N=\frac{2}{3}x^2y^3\left(-\frac{6}{5}xy\right)\)
\(=\left(\frac{2}{3}.\frac{-6}{5}\right).\left(x^2.x\right).\left(y^3.y\right)\)
\(=-\frac{4}{5}x^3.y^4\)