cho tam giác ABC cân tại A, biết A = 90độ, AB = 4cm. tính độ dài cạnh AC, BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

\(\text{Xét}:\)\(\Delta CDE\)\(\text{và}\)\(\Delta CAB\)\(,\)\(\text{ta có:}\)
\(\widehat{C}\)\(:\)\(chung\)
\(\widehat{CDE}=\widehat{CAB}=90^o\)
\(\Rightarrow\Delta CDE\text{∽}\Delta CAB\left(g-g\right)\)
\(\Rightarrow\frac{CD}{DE}=\frac{CA}{AB}\)\(\text{hay}\)\(\frac{2}{DE}=\frac{4}{6}\)
\(\Rightarrow DE=\left(6.2\right):4=3\left(cm\right)\)

tam giác ABC vc tại A (gt) => AB = AC = 4
vì tg ABC vuông nên : AB^2 + AC^2 = BC^2
=> BC^2 = 32
=> BC = \(\sqrt{32}\) do BC > 0

A B C D H 4 1
Làm theo cách lớp 8:
Từ A kẻ AH _|_ BC (H nằm trên BC)
Mà tam giác ABC cân tại A => AH đồng thời là trung tuyến => BH = HC = 1cm
Xét tam giác AHB vuông tại H
=> AH2 = AB2 - BH2 = 42 - 12 = 15cm
=> \(AH=\sqrt{15}cm\)
ΔAHC ~ ΔBDC (g.g) vì:
+ Góc C chung
+ \(\widehat{AHC}=\widehat{BDC}=90^0\)
=> \(\frac{AH}{AC}=\frac{BD}{BC}\Rightarrow BD=\frac{AH.BC}{AC}=\frac{2\sqrt{15}}{4}=\frac{\sqrt{15}}{2}cm\)
Vậy \(BD=\frac{\sqrt{15}}{2}cm\)

Xét \(\Delta AHC\left(\widehat{AHC}=90^o\right)\) có:
\(AC^2=AH^2+HC^2\) (định lí pitago)
\(\Rightarrow AH^2=AC^2-HC^2\)
\(\Rightarrow AH=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{AH^2}-\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}\)
\(\Rightarrow AB=3,75\left(cm\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC=\sqrt{3,75^2+5^2}=6,25\left(cm\right)\)
\(AH=\sqrt{AC^2-HC^2}=3\left(cm\right)\)
\(HB=\dfrac{AH^2}{HC}=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=4+2,25=6,25(cm)
\(AB=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Xét ΔABC có
AD là đường phân giác trong ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{BC}{7}=\dfrac{5}{7}\)
Do đó: \(\dfrac{BD}{3}=\dfrac{5}{7}\)
hay \(BD=\dfrac{15}{7}cm\)
Vậy: \(BD=\dfrac{15}{7}cm\)
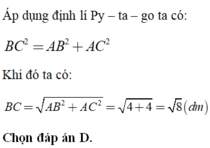
\(\Delta\) cân tại A nên: AB = AC
mà AB = 4 \(\Rightarrow\) AC = 4
Áp dụng định lí Pytago, ta có
\(BC^2=AB^2+AC^2=4^2+4^2\\ =\sqrt{16+16}=4\sqrt{2}\)