Tìm giá trị nhỏ nhất của \(B=3a+\dfrac{5}{a^2}\left(Vớia\ge3\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
1
15 tháng 2 2022
đề bài sai nha bạn vì nếu a=0 thì ko thực hiện được phép tính nha
2
29 tháng 9 2023
`a)D` xác định `<=>a-1 ne 0<=>a ne 1`
`b)` Với `a ne 1` có:
`D=([a-1]/[a^2+a+1]-[1-3a+a^2]/[(a-1)(a^2+a+1)]-1/[a-1]).[1-a]/[a^2+1]`
`D=[(a-1)^2-1+3a-a^2-a^2-a-1]/[(a-1)(a^2+a+1)].[-(a-1)]/[a^2+1]`
`D=[a^2-2a+1-1+3a-a^2-a^2-a-1]/[(-a^2-1)(a^2+a+1)]`
`D=[-a^2-1]/[(-a^2-1)(a^2+a+1)]=1/[a^2+a+1]`
`c)` Với `a ne 1` có:
`1/D=1/[1/[a^2+a+1]]=a^2+a+1=(a+1/2)^2+3/4`
Vì `(a+1/2)^2 >= 0 AA a ne 1`
`=>(a+1/2)^2+3/4 >= 3/4 AA a ne 1`
Hay `1/D >= 3/4 AA a ne 1=>1/D _[mi n]=3/4`
Dấu "`=`" xảy ra `<=>a=-1/2` (t/m).
S
27 tháng 8 2021
a) \(\sqrt{4\left(a-3\right)^2}=2\left(a-3\right)=2a-6\)
b) \(\sqrt{a^2\left(a+1\right)^2}=a\left(a+1\right)=a^2+a\)
c) \(\sqrt{\dfrac{16a^4b^6}{128a^6b^6}}=\sqrt{\dfrac{1}{8a^2}}=\dfrac{1}{\sqrt{8}\left|a\right|}=\dfrac{1}{-\sqrt{8}a}=\dfrac{-\sqrt{8}}{8a}\)
27 tháng 8 2021
a: \(\sqrt{4\left(a-3\right)^2}=2\cdot\left(a-3\right)=2a-6\)
b: \(\sqrt{a^2\left(a+1\right)^2}=a\left(a+1\right)=a^2+a\)
c: \(\dfrac{\sqrt{16a^4b^6}}{\sqrt{128a^6b^6}}=\sqrt{\dfrac{16a^4b^6}{128a^6b^6}}=\sqrt{\dfrac{1}{8a^2}}=\sqrt{\dfrac{2}{16a^2}}=-\dfrac{\sqrt{2}}{4a}\)
31 tháng 10 2021
\(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\\ A_{min}=\dfrac{1}{9}\Leftrightarrow x=\dfrac{3}{5}\\ B=\dfrac{2009}{2008}-\left|x-\dfrac{3}{5}\right|\le\dfrac{2009}{2008}\\ B_{max}=\dfrac{2009}{2008}\Leftrightarrow x=\dfrac{3}{5}\\ C=-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\le1\dfrac{2}{3}\\ C_{max}=1\dfrac{2}{3}\Leftrightarrow\dfrac{1}{3}x=-4\Leftrightarrow x=-12\)
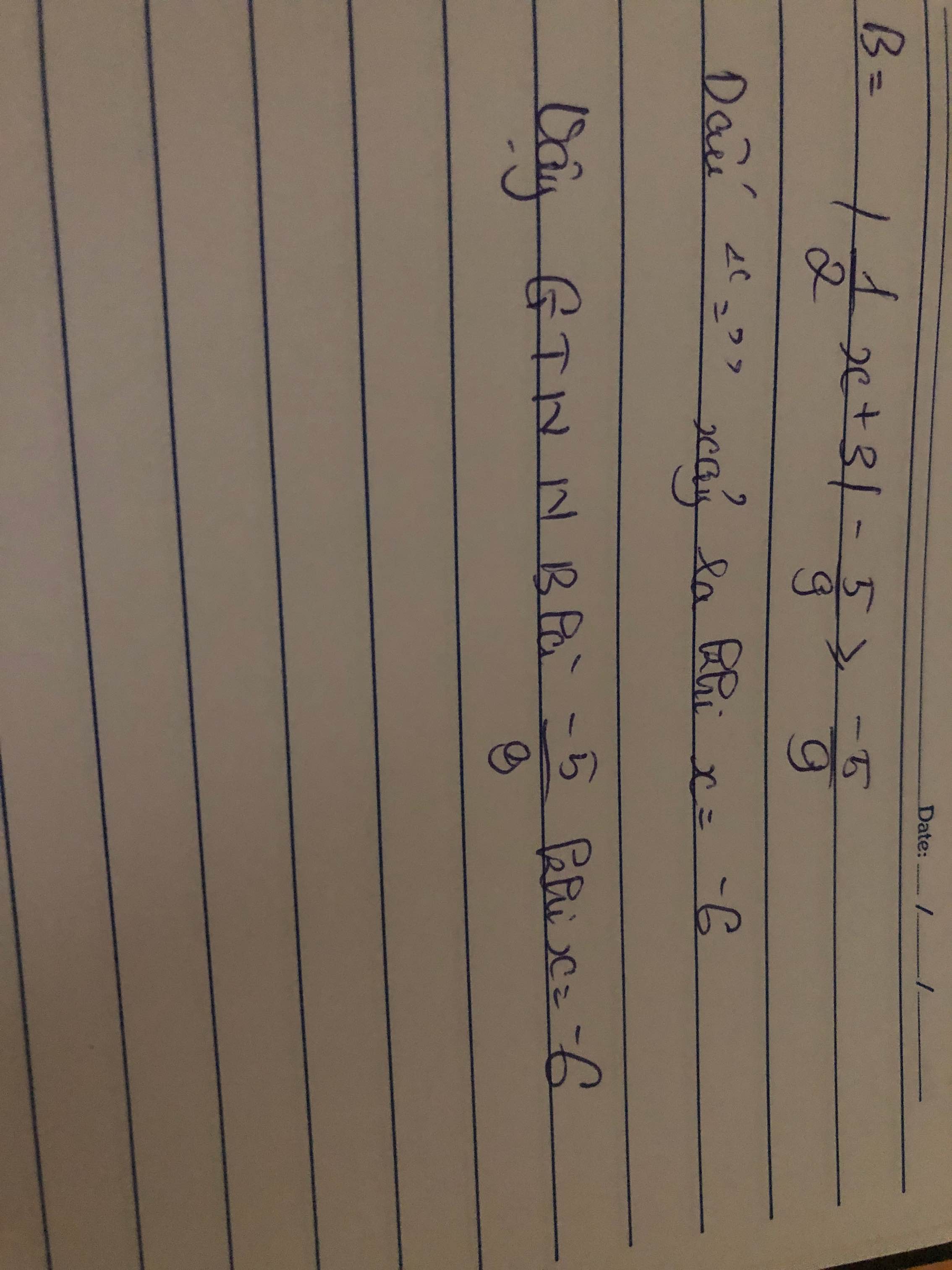
B=a+a+a+\(\dfrac{27}{a^2}-\dfrac{22}{a^2}\)\(\ge\)\(3\sqrt[3]{\dfrac{a.a.27}{a^2}}+a-\dfrac{22}{a^2}\)\(\ge\)9+3-\(\dfrac{22}{9}\)=\(\dfrac{86}{9}\)
vậy MinB=\(\dfrac{86}{9}\) dấu bằng xảy ra khi a=3