Cho \(A=a-\sqrt{a}\). Biết a>1, hãy so sánh A với \(\left|A\right|\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
24 tháng 8 2023
a)
ĐK: \(a>0\)
\(P=\dfrac{\sqrt{a}\left(\sqrt{a}^3+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\\ =\sqrt{a}\left(\sqrt{a}+1\right)-\left(2\sqrt{a}+1\right)+1\\ =a+\sqrt{a}-2\sqrt{a}-1+1\\ =a-\sqrt{a}\)
b)
\(a>1\Rightarrow\sqrt{a}-1>0\Rightarrow\sqrt{a}\left(\sqrt{a}-1\right)>0\)
\(\Rightarrow\left|P\right|=P\)
6 tháng 2 2022
a) \(P=\dfrac{\sqrt{a}\left[\left(\sqrt{a}\right)^3+1\right]}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)
\(P=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\left(2\sqrt{a}+1\right)+1\)
\(P=\sqrt{a}\left(\sqrt{a}+1\right)-\left(2\sqrt{a}+1\right)+1\)
\(P=a+\sqrt{a}-2\sqrt{a}-1+1\)
\(P=a-\sqrt{a}\)
b) Với a > 1 thì \(a>\sqrt{a}\) , do đó \(P=a-\sqrt{a}>0\), suy ra \(\left|P\right|=P\)
c) \(A=a-\sqrt{a}=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Vậy A nhỏ nhất bằng \(-\dfrac{1}{4}\) khi cà chỉ khi \(\sqrt{a}=\dfrac{1}{2}\) hay \(a=\dfrac{1}{4}\)
6 tháng 2 2022
a: \(P=\sqrt{a}\left(\sqrt{a}+1\right)-2\sqrt{a}-1+1=a-\sqrt{a}\)
b: a>1 nên P>0
\(\Leftrightarrow P=\left|P\right|\)
29 tháng 4 2021
Với \(x>0;x\ne1\)
\(M=\left(\frac{1}{a-\sqrt{a}}+\frac{1}{\sqrt{a}-1}\right):\frac{\sqrt{a}+1}{a-2\sqrt{a}+1}\)
\(=\left(\frac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\frac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\frac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)^2}\)
\(=\frac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\frac{\sqrt{a}-1}{\sqrt{a}}\)
\(=1-\frac{1}{\sqrt{a}}< 1\)hay M < 1
18 tháng 5 2021
a,Với \(a>0;a\ne1\)
\(M=\left(\frac{1}{a-\sqrt{a}}+\frac{1}{\sqrt{a}-1}\right):\frac{\sqrt{a}+1}{a-2\sqrt{a}+1}\)
\(=\left(\frac{\sqrt{a}-1+a-\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)^2}\right).\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\frac{a-1}{a+\sqrt{a}}\)
b, Ta có : \(1=\frac{a+\sqrt{a}}{a+\sqrt{a}}\)mà \(a-1=\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)\)
\(a+\sqrt{a}=\sqrt{a}\left(\sqrt{a}+1\right)\)vì \(\sqrt{a}-1< \sqrt{a}\)
Vậy \(\frac{a-1}{a+\sqrt{a}}< 1\)hay \(M< 1\)
CC
0
19 tháng 11 2017
\(M=\left(\frac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\frac{1}{\sqrt{a}-1}\right):\frac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)^2}\)
\(=\frac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}.\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\)
\(=\frac{\sqrt{a}-1}{\sqrt{a}}=\frac{\sqrt{a}}{\sqrt{a}}-\frac{1}{\sqrt{a}}=1-\frac{1}{\sqrt{a}}\)
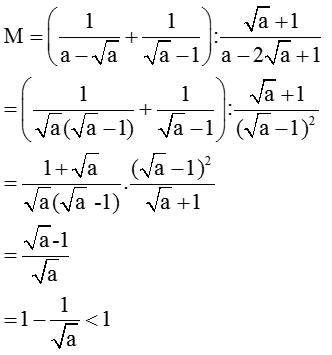
Kudo Shinichi CTV, bn ơi đề bài cho a>1 mà??