cho hình thoi ABCD có AC 12cm BD 6cm tinhchu vi hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chu vi hình thoi là :
( 12 + 16 ) x 2 = 56 ( cm )
Đáp số : 56 cm
Cạnh là: \(AB^2=\left(\frac{12}{2}\right)^2+\left(\frac{16}{2}\right)^2=100\)
\(\Rightarrow AB=\sqrt{100}=10\)
=> AB = 10cm
SABCD: 1/2 . 12 . 16
Chu vi là: \(\frac{\left(\frac{1}{2}.12.16\right)}{10}=9,6\) (c,m)
Vậy:...

A B C D O AC = 8 BD = 6
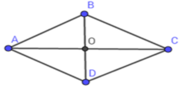
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............


Hướng dẫn giải:
Diện tích hình thoi là:
12 x 5 : 2 = 30 ( c m 2 )
Đáp số: 30 c m 2 .

Ta có: AC = 2AO = 2.12 = 24cm
SABCD = 1 2 BD.AC
=> BD = 2 S A B C D A C = 2.168 24 =14(cm)
=> BO = 1 2 BD = 1 2 .14 = 7(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)
Đáp án cần chọn là: C

chu vi của hình thoi là:
\(5\times4=20\left(cm\right)\)
A B C D
BD,AC CHO HƠI THỪA Á

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B
chuc mung nam moi
mk đang lam đoi xiu