Nêu quy tắc giải bất phương trình ax +by = <_c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2017
+ Ta vẽ đường thẳng (d): ax+by=c
+ Chọn điểm M(x0,y0) ∉ (d) (thường là điểm (0,0)) và tính giá trị ax0 + by0
+ Nếu ax0 + by0>c thì nửa mặt phẳng bờ (d) chứa M(x0,y0) là tập hợp các điểm mà tọa độ của nó là nghiệm của bất phương trình.
+ Nếu ax0 + by00,y0) là tập hợp các điểm có tọa độ là nghiệm của bất phương trình.
CM
13 tháng 11 2017
- Vẽ đường thẳng (d): ax + by = c.
- Chọn điểm M(xo, yo) không thuộc (d) (thường chọn điểm (0; 0)) và tính giá trị axo + byo.
- So sánh axo + byo với c:
+ Nếu axo + byo < c thì tọa độ điểm M thỏa mãn bất phương trình nên miền nghiệm là nửa mặt phẳng bờ (d) (tính cả đường thẳng d) chứa điểm M
+ Nếu axo + byo > c thì tọa độ điểm M không thỏa mãn bất phương trình nên miền nghiệm là nửa mặt phẳng bờ (d) (tính cả đường thẳng d) không chứa điểm M.
7 tháng 3 2022
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
PT
1
CM
12 tháng 1 2019
1,5x > -9
⇔ 
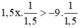(Nhân cả hai vế với 
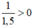, BĐT không đổi chiều).
⇔ x > -6
Vậy bất phương trình có tập nghiệm x > -6
PT
1
CM
9 tháng 9 2017
–x > 4
⇔ (-x).(-1) < 4.(-1) (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).
⇔ x < -4.
Vậy bất phương trình có tập nghiệm x < -4.
PT
1
CM
9 tháng 2 2019
0,3x > 0,6
⇔ 
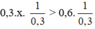(Nhân cả 2 vế với 
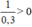, BĐT không đổi chiều).
⇔ x > 2.
Vậy BPT có tập nghiệm x > 2.
PT
1
CM
8 tháng 10 2019
-4x < 12
⇔ 
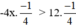(Nhân cả 2 vế với 
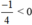, BĐT đổi chiều).
⇔ x > -3.
Vậy BPT có tập nghiệm x > -3.
PT
1
CM
14 tháng 7 2019
2x < 24 ⇔ 2x.1/2 < 24.1/2 (nhân cả hai vế với 1/2 > 0
⇔ x < 12
Vậy tập nghiệm của bất phương trình 2x < 24 là {x|x < 12}
PT
1
CM
5 tháng 8 2017
x - 5 > 3
⇔ x > 3 + 5 (chuyển -5 từ vế trái sang vế phải và đổi dấu thành 5)
⇔ x > 8.
Vậy nghiệm của bất phương trình là x > 8.